티스토리 뷰
[SLAM] 양정연 교수 SLAM 강의 5강. Jacobian Matrix-based Mobile Robot Movement
무엇보다_빛나는_샤트 2022. 2. 20. 16:082021.4.7. 01:45
안녕하세요
프로그래밍을 배우는 빛나는 샤트입니다.
SLAM 강의 5번째. Jacobian Matrix-based Mobile Robot Movement
*이 포스팅은 목원대학교 양정연 교수님의 SLAM강의 유튜브 영상을 보고 제작되었음을 밝힙니다.
출처: 5강. Jacobian Matrix-based Mobile Robot Movement
5강. Jacobian Matrix-based Mobile Robot Movement
🎉강의요약
1. 자코비안 행렬에 대한 복습과 모바일 로봇 각 바퀴의 각속도를 알면 로봇을 제어할 수 있는 수식 복습.
2. 학습했던 수식을 이용해 코드로 구현해 시뮬레이션 시연(이번 강의의 메인)
3. 계속 언급되었던 바퀴의 각속도를 입력으로 활용해 로봇의 제어를 눈으로 확인!
4. 왼쪽/오른쪽 바퀴의 각속도를 다르게 입력해 회전하는 것을 눈으로 확인!
5. 또한 가장 중요한 DPI fuction. (로봇이 회전을 할 때 효율적인 제어를 하기 위한 함수)
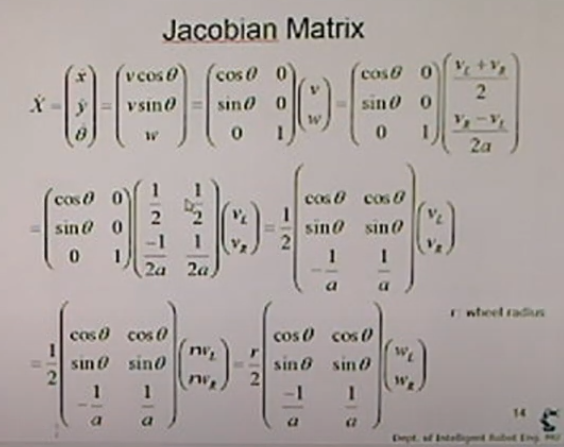
<Jacobian Matrix>
이전 강의에서 배운 내용 복습
모바일 로봇의 위치는 x,y,θ를 이용해 알 수 있으며, 이를 미분하면 위치의 변화량을 구할 수 있다. (로봇의 각도와 각 바퀴의 각속도, 축간거리(a), 바퀴 반지름(r) 알고 있을 때)

<Ex) rover1.py Graphical Movement>
rover.py를 이용해 바퀴의 각속도(좌측, 우측 독립적으로)를 이용해 모바일 로봇(Path Finder)를 제어할 수 있다.
3DS개체를 불러와 호모지니어스 트랜스폼을 어떻게 대입해서 움직일 것인지 다룰 수 있다.
(편집자 주: 정식 수업을 들은 것이 아니라 파일 등을 구할 수 없어서 아쉽다)
*move 함수
입력으로 x,y,q를 받아 로봇의 움직임을 제어.
여기서 주의할 사항: 호모지니어스 트랜스폼->순수한 translation 이후에 (새로운 좌표계에서)회전(회전 후에 translation하게 되면 복잡해지기 때문)
self.robot이 3차원 객체이기 때문에 여기에 translation인 T와 호모지니어스 H를 곱해서 move함수 완성
Simulation Environment
*Path Finder: 시뮬레이션으로 구현한 로봇이며, 실제로 화성에 탐사를 떠나 많은 과학자(뿐만 아니라 일반 대중들도)기대했지만 일주일 만에 죽었다는...
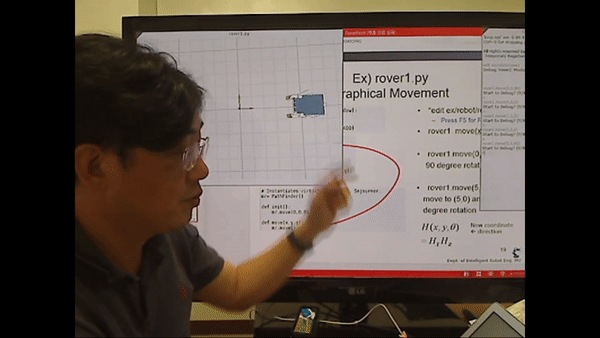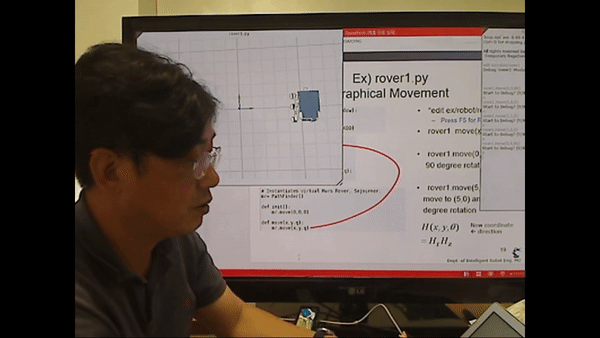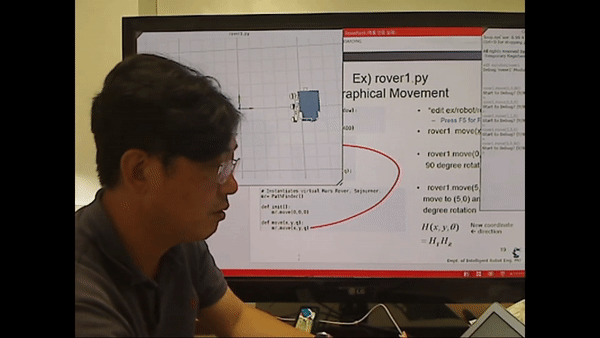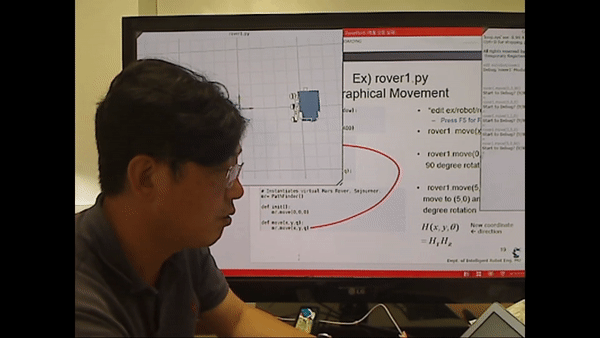
<시뮬레이션 시연>
각도를 이용해 로봇의 회전을 시연하는 모습
시뮬레이션 툴을 이용해 로봇을 제어하는 모습을 확인하려면 영상의 아래 시간대를 확인.
8:35~11:14 (로봇과 시뮬레이션 환경 설명)
11:15~12:05 (로봇 회전 시뮬레이션 시연)


<robver2.py>
자코비안 행렬이 추가되어 있다.
수식을 코드로 구현함. (5_6 참고)
1)fk함수
- w_L, w_R는 바퀴의 변위이며 J(자코비안)함수 대입
-> 양쪽 바퀴 각도 차이를 입력하면 자코비안을 풀면 dx, dy, dq 나옴
-> 현재 좌표와 각도에 더해져서 결국 로봇이 움직이게 되는 코드
2) J함수
- self.q는 heading angle
- dx, dy, dq를 구할 수 있다.
❗여기서 각도 제어 중 0도, 360, 720도 등...모두 결과는 제자리인 상태이지만 회전을 하기 때문에 이는 불필요하다❗
>> 이를 해결하기 위한 방법: DPI 함수

<DPI Fuction>
❗매우 중요❗
각도를 0~360도 사이로 할 것인지, -180~180도 사이로 할 것인지 결정해야 함.
예시: 현재 각도가 170도이고 목표는 -170라면 e = θ_d - θ에 의해 e = -340이 나오게 되지만 실제 효율적인 움직임은 +20도이다. 사전에 -180~180도 사이라고 정의했다면 알아서 20도로 변하는 작업이 필요.
예시 문제에서는 -340이므로 +360을 해줘서 -180~180 사이인 지 확인. 만약 +340이라면 -360을 해줘서 -180~180 사이에 오는 지를 반복적으로 확인해서 변환하면 된다.
불필요한 움직임을 배제하고 효율적인 움직임 필요하다! (P 컨트롤에서 매우 중요)
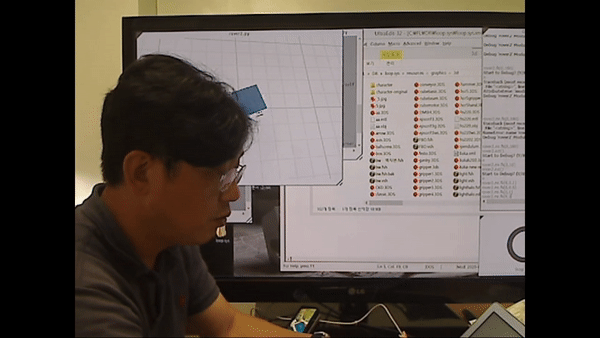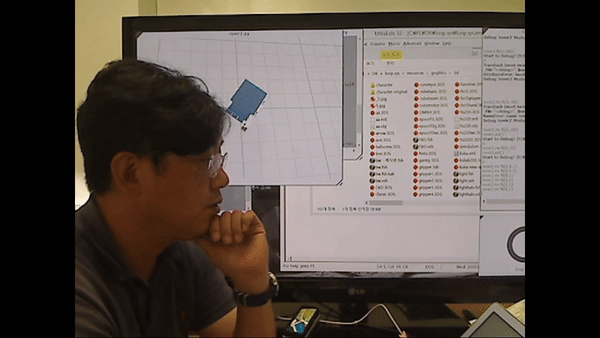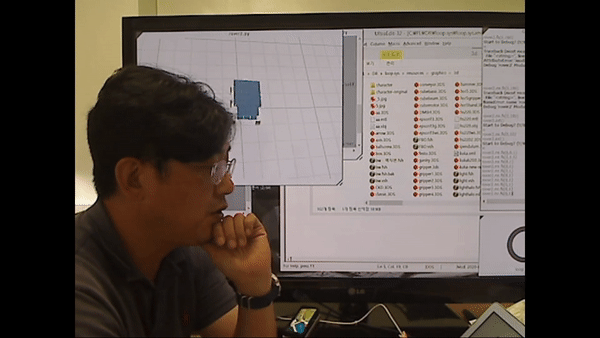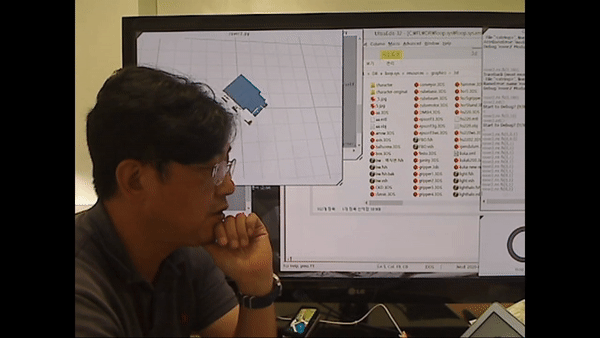
<rover2.py 시연>
로봇의 회전을 제어하는 모습을 확인
시뮬레이션 툴을 이용해 로봇을 제어하는 모습을 확인하려면 영상의 아래 시간대를 확인.
28:21~29:07
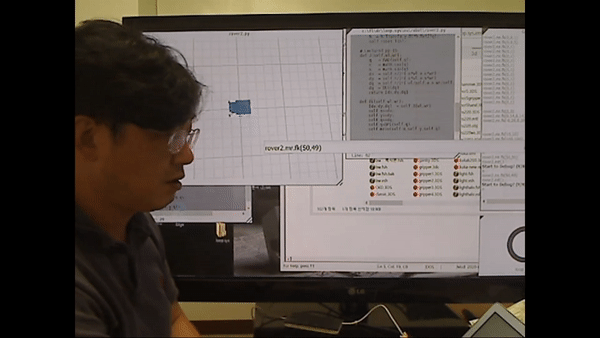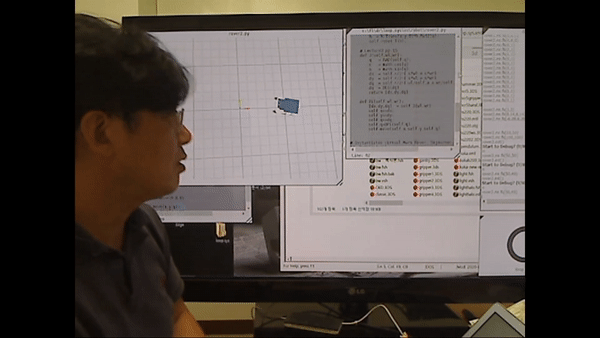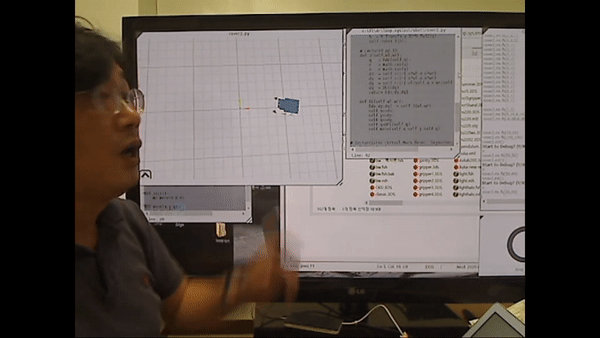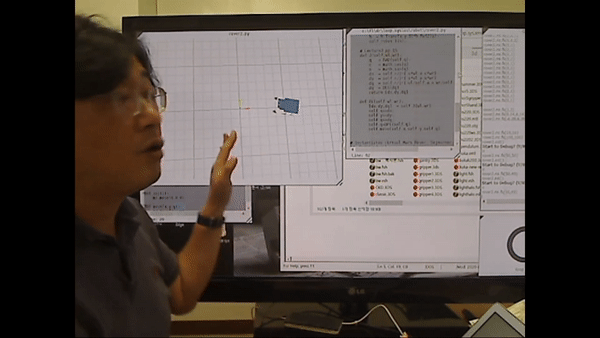
-> 양쪽 바퀴 (독립적으로) 각도를 입력하면 로봇의 움직임을 제어할 수 있다. 양쪽 바퀴의 각도를 다르게 주면 로봇의 turn을 하게 된다.
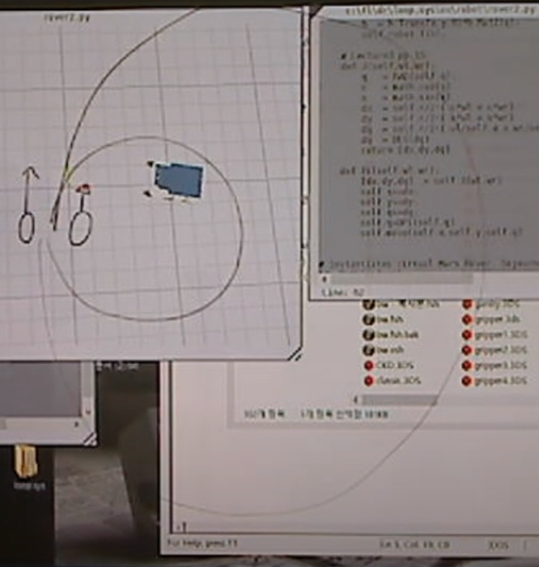
우측 바퀴 각도가 좌측 바퀴 각도 크기 대비 작은 수준으로 작다면 큰 원을 그리며 우회전
반대로 우측 바퀴 각도가 좌측 바퀴 각도 크기 대비 큰 수준으로 작다면 작은 원을 그리며 우회전.
*여기서 알 수 있든 이러한 작은 각도 차이에 의해 모바일 로봇을 똑바로 전진시키기 어렵다.


<Ex) Forward Kinematics with rover2.py WL=1 and WR=2>
왼쪽 바퀴 각속도가 1, 오른쪽 바퀴 각속도가 2일 때의 코드 구현
=> 좌회전 하는 형태
위의 입력값을 한 번 넣게 되면 각도는 약 11도로 틀어진 상태가 된다.(원점 기준)
한 번 더 넣게 되면 약 22도가 틀어지는 형태가 된다. (원점 기준)
=> 즉,w_L=1, w_R=2를 계속 넣게 되면 좌회전을 하며 원을 그리는 형태가 된다.
(참고 지식)
*PI제어: 속도제어
*PD제어: 시간당 위치 제어

<rover3.py for Control Loop>
While문이 True로 무한 루프가 돈다.
fk(forward kinematics)를 계속 걸어준다.
시간은 점점 흘러가고, 10초 만큼 sleep.
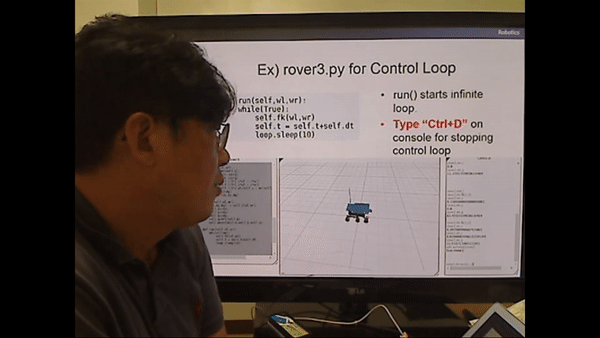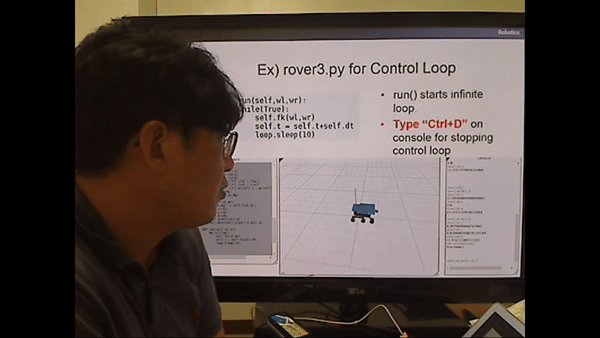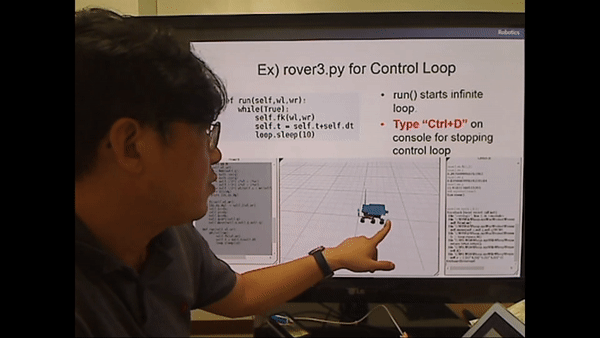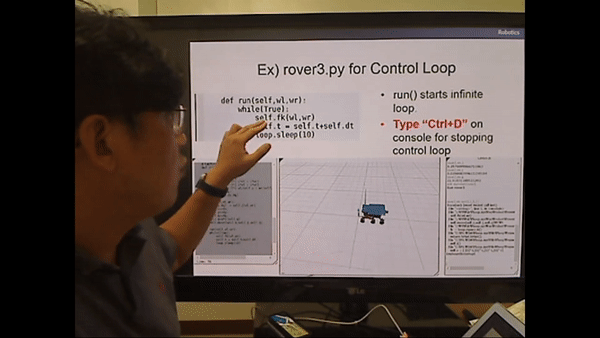

<로봇 전진 시뮬레이션>

<로봇 회전 시뮬레이션>

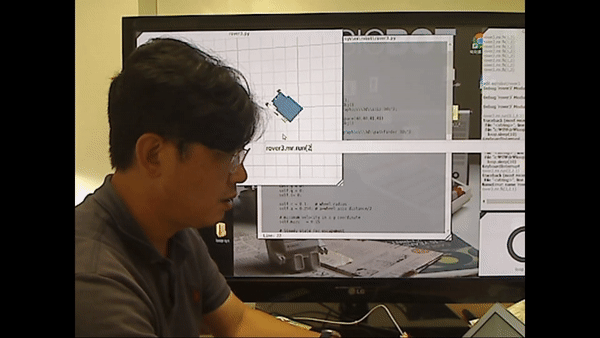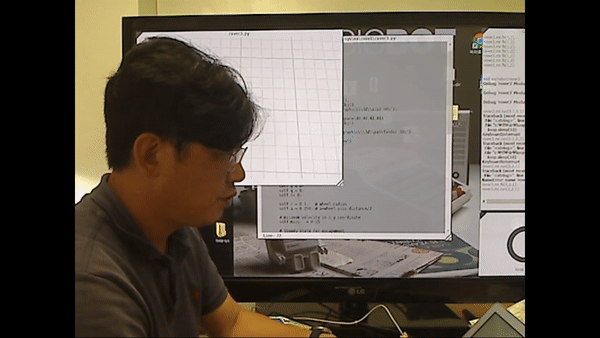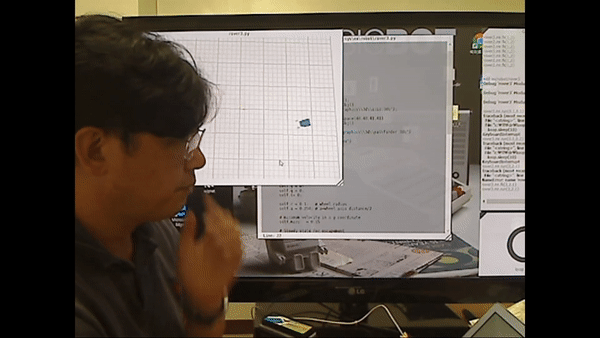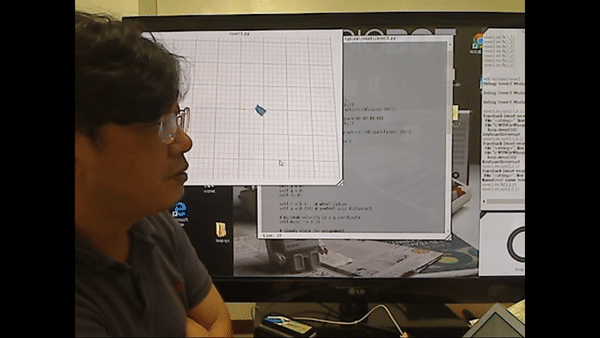
입력값에 따라 연속적으로 움직이는 모습 확인
*영상 속 타임라인: 41:12~41:47
이는 태양과 지구의 공전과도 비슷하다. 지구는 직진하려고 하지만 태양이 조금 잡아당겨서 결국은 작은 힘이지만 끌어당기기 때문에 매우 큰 원으로 태양 주위를 회전한다.
💡강의 후 느낀 점
이전 강의에서 배운 내용을 시뮬레이션 해보는 시간이었는데 코드 구현 부분이 영상이 조금 흐릿해서 조금 아쉬웠다.
하지만 실제로 로봇이 움직이는 모습을 눈으로 확인하고 이론으로만 듣던 사실을 확인해 볼 수 있었다.
특히 바퀴의 각속도의 입력만으로 로봇을 움직일 수 있다는 점을 실제로 봐서 더 신기했다.
(물론 그 반대는 어렵지만)
그 중에서 두 바퀴의 각속도 차이가 매우 작을 때 큰 원을 그리고 회전하는 내용과 태양계의 공전과 연관짓는 내용은 인상적이었다.
자율주행 모바일 공부하다가 천문학까지 확장?!
피드백은 언제나 환영합니다.😊
틀린 부분 있다면 지적해주시고 도움이 되었다면 댓글과 공감 눌러주세요.
'SLAM' 카테고리의 다른 글
- Total
- Today
- Yesterday
- AIFFEL인공지능과정
- 인공지능
- 모두의연구소
- 서빙로봇
- 자율주행로봇
- 실내자율주행
- 인공지능 교육
- 광주인공지능사관학교
- 자율주행기술
- Python
- 멋쟁이사자처럼
- ros
- 도전
- 배달로봇
- 광주
- AIFFEL
- 양정연SLAM
- SLAM강의
- 대전 인공지능
- AIFFEL후기
- 해커톤
- 멘탈관리
- AIFFEL교육
- 모두의 연구소
- IT
- 아이펠
- 인공지능교육
- SLAM공부
- Slam
- 광주AI
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |

