티스토리 뷰
2021. 10. 8. 17:34
안녕하세요
프로그래밍을 배우는 빛나는 샤트입니다.
SLAM 강의 25강. Why we need Observation?
*이 포스팅은 목원대학교 양정연 교수님의 SLAM강의 유튜브 영상을 보고 제작되었음을 밝힙니다.
출처: 25강. Why we need Observation?
25강. Why we need Observation?
🎉강의요약
1. y = Cx + Du 식에서 C=1, D=0이라면 노이즈가 없는 선형 시스템
2. 하지만 실제 세계에서는 항상 노이즈가 있다.
3. 시스템 dynamics에 영향을 주는 Process Noise
4. 관측에 영향을 주는 Measurement Noise
5. 인코더의 값이 관절의 각도를 의미하는 것이 아니다. 즉, 측정값이 실제 값과 일치하지 않는다. (노이즈 때문)

<Feedback Observation>
상태 공간에 대한 방정식: x는 변수 하나가 아니라 벡터, x변수 안에는 속도가 포함.
x^ = Ax + Bu
x는 벡터이기 때문에 2차식이 1차식처럼 보이게 해준다.
u는 입력. PID제어기를 쓰는 경우 토크.
*행렬A의 Eigenvalue가 음수라면 수렴
y = Cx + Du
우리가 관측한 값(y)은 인코더의 값.
인코더의 값을 각도로 치환하기에는 백래쉬, 노이즈 등으로 어렵다.
y=x라면 관측한 값이 그대로 데이터와 같다. C=1.D=0 (이상적인 상황)
y는 관측의 개념. x는 우리가 원하는 상태(θ^, θ^^)가 아닐 수 있고
y= f(x): 인코더와 관절 사이의 어떠한 함수 관계가 있다면 이렇게 표현한다.
움직임이 있을 때 관측값이 달라진다. 중력에 의해 상하 움직임은 다르게 생각.
y는 센서값. 입력에 의해 x가 변할 수 있다면 D는 0이 아니다.
SLAM 영역에서는 관측한 영역과 실제는 다르다.
관측을 토대로 실제 값을 알기 어렵다.
에러가 존재하는 환경에 대해 학습.
자율주행 영역에 들어오기 전에 세상은 프로그래밍할 수 있다고 생각했겠지만
움직이려다보니 슬립 등 다양한 변수의 세계관에 들어간다.
조인트 앵글을 제어하기 위해선 θ^가 필요한데 실제 측정하는 것은 Encoder값(y)이다.

<2nd order Mass-Spring-Damper>
x는 위치, x^는 속도
외곽에서 스프링을 쫙 당겨서 놓은 모양.
시간t에 대해서 exp하게 줄어들고 있다.

<Our model is Perfect? No, it has uncertainties and Model is Imperfect>
비선형 -> 선형화 시켜서 풀려고 노력.
X^ = AX + Bu는 불안정. -> 선형적으로 변환 노이즈(N)를 더한다.
시스템 dynamics에 영향을 주는 Process Noise
X^ = AX + Bu + N
uncertainties(불확실성): 마찰 등(윤활유가 증발)
관측 Y = CX + Du
도 마찬가지로 노이즈(N') 추가. N': 측정 오차(관측에 영향을 주는 Noise)
예시) 전기가 60Hz라면 그 주변에서 흔들린다.

<KF model>
X^ = AX + Bu와 비슷한 수식이다.
1. x = Fx + Bu +wk
wk는 Process Noise
맨 위의 수식에서 B가 0인 경우라고 생각하면 된다.
2. Z = Hx + vk ->
vk는 Measurment Noise

<Process Noise>
N을 추가한 형태
코드로 구현한 모습 -> 그래프를 확인.
코드에서 Na, Nv는 가속도와 속도를 나타내고 손으로 쓴 수식을 살펴보면
X라는 행렬은 x^, x^^로 이루어져 있다.
즉 Na는 x^^, Nv는 x^를 의미하며 0.1*가우시안 노이즈를 추가한 형태
>> 겨우 0.1이지만 그래프가 지저분하게 움직인다 -> 이것이 자연계
Process Noise는 측정할 수 없고 모델링을 할 수 없고 감소하는 방향으로 해야 한다.
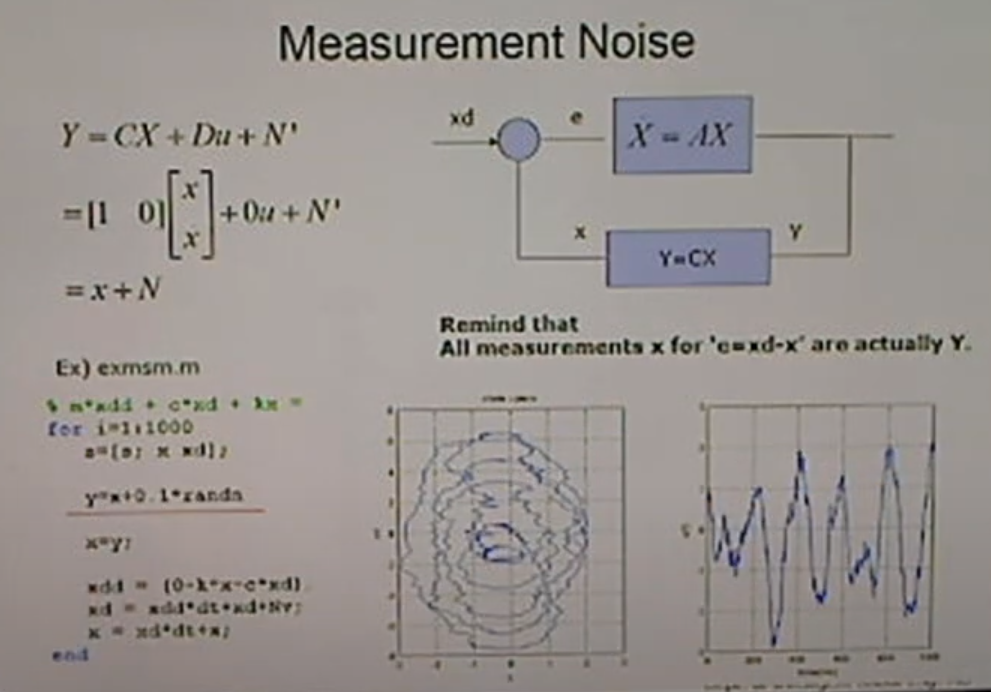
<Measurement Noise>
오른쪽 위 그림은 외력이 0이므로 X^ = AX + Bu에서 Bu는 0이 된다.(u=0)
Y=CX도 마찬가지의 개념으로 표현한 것
즉 Y = x + N
아래 코드를 보면 y = x + 0.1*randn()인데, C=1이라는 간단한 상황.
x는 실제로 y와 같아야 하지만 노이즈를 추가함.
문제 풀이->아까보다 더 심하다. 수렴해서 0으로 점점 되어야 하지만 발산하는 모양이다. 진폭이 더 커짐.
>> 관측오차가 커지면 제어하기 어려운 시스템. 센서에 노이즈가 들어가면 매우 힘들어진다.(위험하다)

<Process and Measurement Noises are UNAVOIDABLE Problems>
선형 시스템은 제어하기 쉽다. 노이즈가 없기 때문.
인코더는 완벽하지만 관절각도를 의미하는 것은 아니다. 프레임이 단단(Stiffness)한 것이 좋다. 저주파에서 흔들리지 않도록. 만약 Stiffness가 낮다면 더욱더 어렵다.
관측할 수 있는 것은 완벽하지 않다. 초음파, 적외선 등 좋지 않다.
>> SLAM은 예상하지 못했던 부분들이 더 많이 있다.
피드백은 언제나 환영합니다.😊
틀린 부분 있다면 지적해주시고 도움이 되었다면 댓글과 공감 눌러주세요
'SLAM' 카테고리의 다른 글
| [SLAM] 양정연 교수 SLAM 강의 27강. Prediction in KF (0) | 2022.02.21 |
|---|---|
| [SLAM] 양정연 교수 SLAM 강의 26강. Introduction to Kalman Filter (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 24강. From math equation to State Equation (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 23강. Observation (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 22강. Non Parametric Method (0) | 2022.02.21 |
- Total
- Today
- Yesterday
- 인공지능 교육
- SLAM공부
- 멘탈관리
- 모두의 연구소
- Slam
- 모두의연구소
- 인공지능교육
- SLAM강의
- AIFFEL후기
- 실내자율주행
- 서빙로봇
- 양정연SLAM
- 멋쟁이사자처럼
- 대전 인공지능
- 해커톤
- 광주인공지능사관학교
- 도전
- Python
- IT
- 배달로봇
- 광주AI
- 자율주행로봇
- ros
- AIFFEL인공지능과정
- 아이펠
- AIFFEL교육
- 광주
- 인공지능
- AIFFEL
- 자율주행기술
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
