티스토리 뷰
[SLAM] 양정연 교수 SLAM 강의 29강. From Kalman Filter to Particle Filter
무엇보다_빛나는_샤트 2022. 2. 21. 21:252021. 10. 10. 20:41
안녕하세요
프로그래밍을 배우는 빛나는 샤트입니다.
SLAM 강의 29강. From Kalman Filter to Particle Filter
*이 포스팅은 목원대학교 양정연 교수님의 SLAM강의 유튜브 영상을 보고 제작되었음을 밝힙니다.
출처: 29강. From Kalman Filter to Particle Filter
29강. From Kalman Filter to Particle Filter
🎉강의요약
1. Kalman Filter의 기본 구조: 관측-추정-예측
2. Process Noise를 추가한 입력이기 때문에 이를 잘 잡아줘야하며 칼만 필터가 매우 우수
3. Tracking 문제에서는 칼만 필터는 선택이 아닌 필수
4. 칼만 필터는 선형 구조(덧셈으로 이루어짐)이므로 비선형 환경을 위해 Particle Filter 필요

<Understanding Matlab Code with K.F. 3. Correction(Update Estimate)>
X^(현재값)을 이용해 예측값(X^`)을 구한다
P를 알고 있다면 (초기에는 0) 수식을 통해서 P`을 구한다.
관측값Z를 이용해 X^을 구한다.
>> K값을 구할 수 있다.
같은 과정을 계속 반복한다.
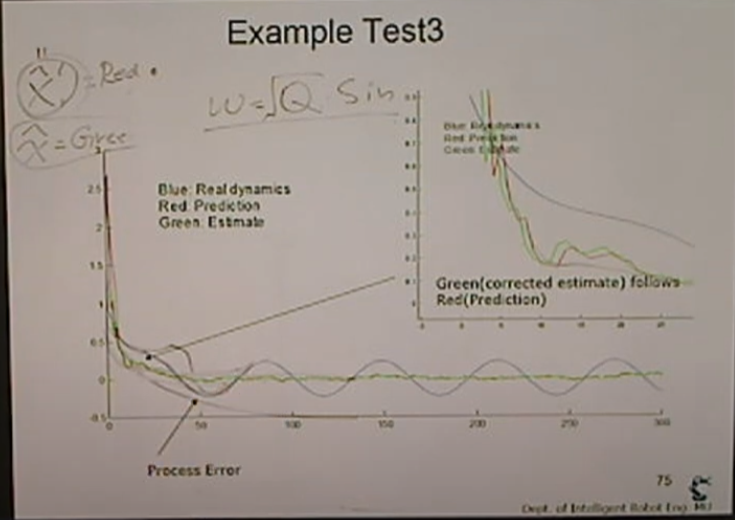
<Example Test3>
x_dot = x + w (w는 sin 노이즈)
z = x + v (v~N(0,1))
결국 0이 되어야하는데 되지 못하는데 w가 있기 때문.
그래프의 파란선은 진짜 값. (출렁)
> 수렴을 못하게 하도록 w가 사인 파형
이런 경우는 실제로 많다.
노이즈가 많다.
빨간선은 칼만 필터를 적용한 예측.
초록선은 추정값.
파랑>빨간>초록으로 어떻게 되는지 확인.
빨간선과 초록선의 격차는 매 구간마다 다르다.
covariance가 달라지기 때문에
파란선과 초록선의 오차가 사라지게 된다.
(process noise 제거)
하지만 좌측 하단의 공간: exp하게 가려다가 노이즈때문에 출렁.
>> 칼만 필터가 잘 제어한다.
파란색을 쫓아가는것이 아니라 노이즈를 잘 피해야 한다.
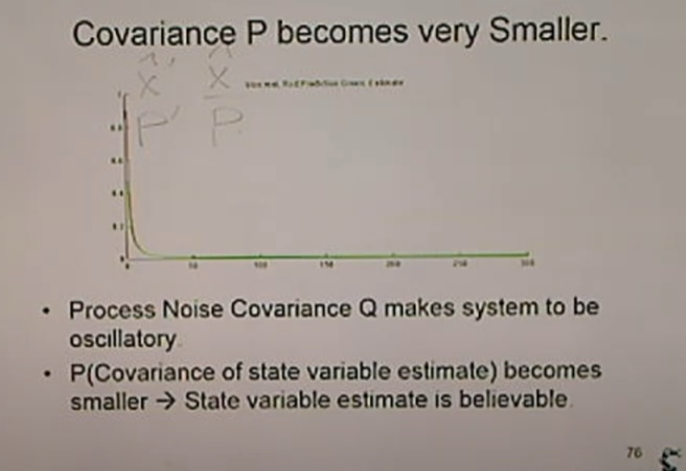

<Covariance P become very Smaller>
그럼 이번엔 P를 알아보면,
실제 데이터는 많이 흔들리지만 잘 잡아내고 있다.
빨리 내려와서 수렴. Covariance가 매우 작다.


<Why Kalman Filter and Particle Filter>
칼만 필터 적용하게 되면 노이즈를 잘 줄여준다.
실제 전후를 비교하면 사람의 중앙이 잘 흔들리지 않는다.
추적하는 문제에는 무조건 사용해야함.

<Probailistic Robotics From KF to PF>
현재 나는 대충 어떤 위치에 있다.
한 발자국 이동하면 아마 어떤 위치 근처에 있을거야.
대충 원점으로부터 거리를 재보니 (z)
보정을 해서 보니 '이정도의 covaraince'를 가지고 있구나.
점점 covariance가 적어져서 위치를 알 수 있다.
칼만필터를 슬램에 적용하기 위해선 문제가 조금 있다.
모두 더하기로 되어 있다: 선형
실제로 자동차의 움직임을 보면 비선형 관계.
> 비선형으로 개선한 것을 Enhanced KF
공간이 커질 수록 연산량이 매우 많아진다.
> 대안이 필요하다.
>> Particle Filter!
칼만필터는 covariance만 등장.
우리가 다루고자 하는 시스템을 확률적으로 볼 수 있어야 한다.

<Now, Localization with Kalman Filter Where am I?(What is Xk=?)>
등대까지의 거리를 관측
관측하면서 거리가 얼마인지는 알 수 없다. (현재 위치를 알기 어렵다)
실내에서 관측이 안 되기도 한다.
정확한 위치(좌표)를 알아야 한다.
고정된 스팟을 이용
> 100m에 legend가 있다는 것을 인지. map을 그려야 한다.(슬램의 어려움)
z=Hx를 이용.
covariance를 더 작게 만들어야 한다 -> 칼만 필터

<Now, Localization with Kalman Filter Where am I?(What is Xk=?)>
새로운 x를 구하고 초기 추정값을 이용해 예측. 관측-추정-예측
covariacne를 줄이는 방향
피드백은 언제나 환영합니다.😊
틀린 부분 있다면 지적해주시고 도움이 되었다면 댓글과 공감 눌러주세요
'SLAM' 카테고리의 다른 글
| [SLAM] 양정연 교수 SLAM 강의 31강. Joint Probability and Conditional Independence (0) | 2022.02.21 |
|---|---|
| [SLAM] 양정연 교수 SLAM 강의 30강. Can we think Kalman Filter with Probability? (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 28강. Kalman Gain in Kalman Filter (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 27강. Prediction in KF (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 26강. Introduction to Kalman Filter (0) | 2022.02.21 |
- Total
- Today
- Yesterday
- 모두의 연구소
- Python
- 인공지능
- IT
- 대전 인공지능
- 아이펠
- 양정연SLAM
- AIFFEL교육
- AIFFEL
- 광주AI
- SLAM공부
- 광주
- Slam
- 자율주행로봇
- 인공지능교육
- 도전
- 멘탈관리
- 실내자율주행
- 광주인공지능사관학교
- 자율주행기술
- 모두의연구소
- AIFFEL후기
- ros
- 해커톤
- 인공지능 교육
- 서빙로봇
- 멋쟁이사자처럼
- 배달로봇
- AIFFEL인공지능과정
- SLAM강의
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
