티스토리 뷰
2021. 10. 5. 23:53
안녕하세요
프로그래밍을 배우는 빛나는 샤트입니다.
SLAM 강의 19강. Bayesian Probabilisty
*이 포스팅은 목원대학교 양정연 교수님의 SLAM강의 유튜브 영상을 보고 제작되었음을 밝힙니다.
출처: 19강. Bayesian Probabilisty
19강. Bayesian Probabilisty
🎉강의요약
1. 문제를 조건부 확률로 볼 필요가 있다.
2. 베이지안 분류기를 이용해 키를 크다? 작다? 분류
3. 데이터를 수집해 특정 값x에 대해 키가 큰지 작은지 알고 싶은 경우 prior, likelihood, evidence를 이용해 구해야 한다.

<Why Posterior Prob. Is very different?>
가위바위보
1. 가위를 낼 Prior 확률: 1/3
2. 2번 연속 가위를 낼 확률은...? 조건부 확률 이용

<Posterior Prob.>
Pr(A|B) = P(A∩B) / P(B)
또한 P(A) = P(B|A)PA(A) 이므로
>> Pr(A|B) = P(B|A)P(A) / P(B)

<Why Posterior Probability? It reduces Classification Errors..>
랜덤값 x가 주어졌을때 C에 속한다 또는 그렇지 않다 라는 것을 판단하는 문제 설계

<Is It Big or Not?>
위쪽 그림은 크다는 것을 판별할 수 있지만 아래는 알 수 없다. 왜냐하면 비교대상이 없기 때문.
일반적인 사과의 크기와 비교해서 크다 라는 생각을 해야 한다.
> 모든 문제를 조건부 확률로 보는 것이 중요.

<Classification: Bayesian Classifier>
키라고 하는 x값. x= 170일때 크다(w1), 아니다(w2)
x축 위에 분포가 있을때 어떤 값이 나올때 키가 큰지 작은지 판별하는 것을 설명
이것을 누가 결정하나? 많은 사람들.
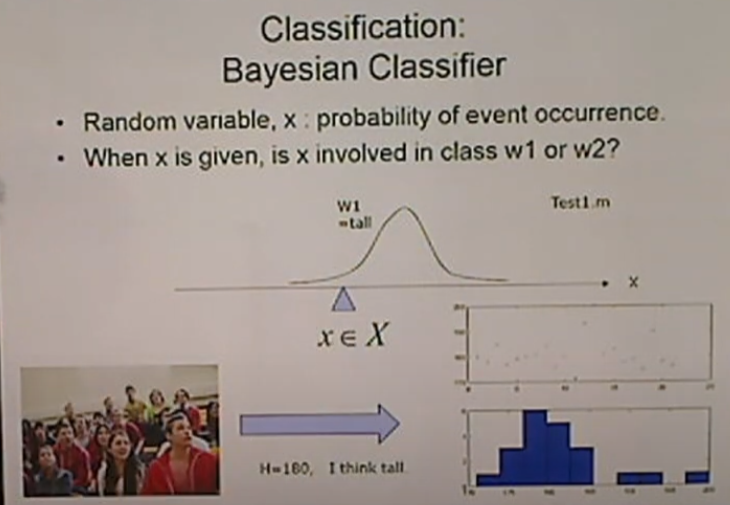
<Classification: Bayesian Classifier> - Test1
키를 데이터로 주고 설문조사. 크다고 생각하는 데이터를 표현(히스토그램)
180 근처에 확률 분포가 형성. 이 데이터를 토대로 평균과 표준편차를 이용해 그래프를 그린다. PDF를 그릴 수 있다.
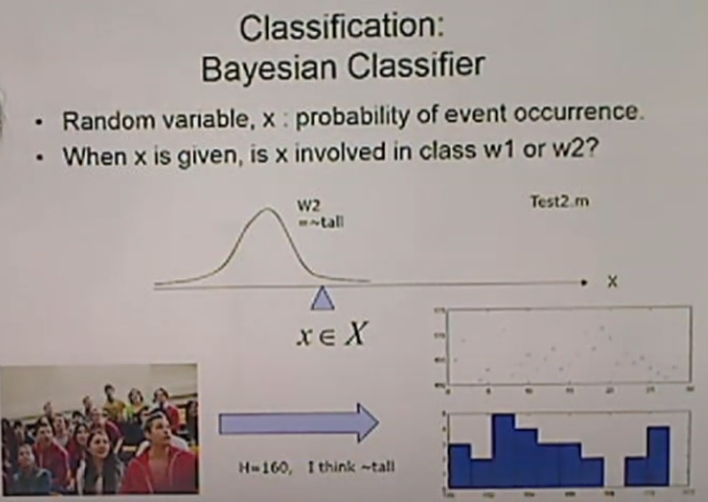
<Classification: Bayesian Classifier> - Test2
H=160일때 히스토그램.
표준편차는 위 그림보다 큰 형태가 된다.
문제를 확률적으로 푸는 법: 거리 센서값일 때 150일때는 장애물이 있는 가능성이 낮다(밀도가 낮다)


<Sample from Surveys>
w1은 키가 크다. w2는 키가 작다.
180 근처면 키가 크다.(표준정규분포에 가깝게)
키가 작다는 의견은 조금 더 넓게. 표준편차가 크다.
수집한 데이터가 가우시안 분포를 가진다고 하면 위와 같이 mean, std를 구할 수 있다. 결과를 확인해보니 w1이 표준편차가 더 크다는 것을 알 수 있다.
예를 들어 x=170이라는 값을 이용할 때 키가 큰 지 작은지 알아보려고 할때, 위 수식에 평균(μ)와 표준편차(σ)를 대입해 나오는 값을 비교해보면 키가 더 큰 것을 알 수 있다.

<Classification: Bayesian Classifier>
Pr(x): 입력x가 큰지 작은지 결정하는 확률
Pr(w2): 예를 들어 w1은 100개, w2는 50개라고 할때, 50/150의 prior 확률
Pr(w2|x): 입력x가 주어졌을때 w2일 확률
Pr(x|w2): w2일때 x일 확률. 키가 작은것들 중에 키가 170일 확률. 키가 작다고 응답한 사람 중에 170은 몇 개나 있나?

<Classification: Bayesian Classifier>
위 그래프는 두 가지.
P(x|w2): w2일때 x의 분포
P(x|w2): w1일때 x의 분포

<Samples>
키가 크다고 생각하는 것들의 x분포가 이러한 커브를 그린다.

<For Bayesian Classifier p(x|w) and p(w) are required.>
P(w1) = w1데이터 / 전체 데이터
P(w2) = w2데이터 / 전체 데이터


<Back to Bayesian Probability>
[오른쪽]위 수식은 위 아래로 동치. likelihood, prior, evidence
[왼쪽]likelihood: 입력x가 있을때 w1의 밀도, w2의 밀도를 비교하는 것
좌측 공식을 이용해 P(w1|x), P(w2|x)를 구한다.
P(x)를 구하는법 필요

<Definition Bayesian Classifier>
Pr(w1|x) > Pr(w2|x)라고 하면 x는 키다 크다(w1) 라고 할 수 있다.
아니라면 키가 작다(w2)라고 할 수 있다.
또한 유의해야할 점은 P(w1), P(w2)를 구할 때 너무 데이터 편차가 큰 경우를 조심해야 한다. P(w1) = 100/101, P(w2) = 1/101

<Finally. P(x)=?>
P(w1|x) + P(w2|x) = 1 을 이용해 구할 수 있다.
즉, 정리한 수식이 위와 같이 구할 수 있다.

<Posterior Probability in General>
최종적인 수식을 위 처럼 구할 수 있다.

<Engineering Notation>
likelihoodness * prior/모든사건
Maxium LIkelihood Estimation: 회귀에서 적용가능
likelihoodness: 모델이 있을 때 그 위에 있는 값들의 분포. 직선이 있을 때 데이터가 어떻게 분포했는지 알 수 있다.
피드백은 언제나 환영합니다.😊
틀린 부분 있다면 지적해주시고 도움이 되었다면 댓글과 공감 눌러주세요
'SLAM' 카테고리의 다른 글
| [SLAM] 양정연 교수 SLAM 강의 21강. Probabilistic Approaches (0) | 2022.02.21 |
|---|---|
| [SLAM] 양정연 교수 SLAM 강의 20강. Bayesian Classifier (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 18-2강. Normal Distribution in 2 Dim. Space (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 18강. Normal Distribution (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 17강. Midterm Exam, Roomba-like Stochastic Navigation (0) | 2022.02.21 |
- Total
- Today
- Yesterday
- SLAM강의
- Python
- SLAM공부
- 해커톤
- AIFFEL
- 실내자율주행
- 자율주행기술
- 자율주행로봇
- 광주AI
- 인공지능교육
- AIFFEL인공지능과정
- AIFFEL교육
- IT
- 아이펠
- 멋쟁이사자처럼
- ros
- 광주인공지능사관학교
- 배달로봇
- 대전 인공지능
- 모두의 연구소
- 도전
- 광주
- 양정연SLAM
- 멘탈관리
- 모두의연구소
- 인공지능
- 인공지능 교육
- 서빙로봇
- Slam
- AIFFEL후기
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
