티스토리 뷰
[SLAM] 양정연 교수 SLAM 강의 33강. Probabilistic Approach of Kalman and Particle Filter
무엇보다_빛나는_샤트 2022. 2. 21. 21:272021. 10. 22. 17:40
안녕하세요
프로그래밍을 배우는 빛나는 샤트입니다.
SLAM 강의 33강. Probabilistic Approach of Kalman and Particle Filter
*이 포스팅은 목원대학교 양정연 교수님의 SLAM강의 유튜브 영상을 보고 제작되었음을 밝힙니다.
출처: 33강. Probabilistic Approach of Kalman and Particle Filter
33강. Probabilistic Approach of Kalman and Particle Filter
🎉강의요약
1. Kalman Filter에서 예측과 업데이트는 서로에게 영향을 준다.
2. 예측은 초기~이전스텝까지의 관측(Z)를 통해서 현재(k)를 알아내고
3. 업데이트는 초기~현재스탭까지의 관측(예측)을 토대로 현재(k)를 알아낸다.
4. 이때 예측을 구하는 식에서 적분이 나오는데 푸는 것이 까다롭다.
5. 이를 해결하고자 입자(Particle)의 개념을 이용해서 점들의 분포를 통해 면적을 구하는 컨셉을 이용한 것이 Particle Filter
6. 점들의 분포를 키우기 위해 Noise를 추가하고 몇개를 제외시켜서 분포를 작게 만드는 과정을 통해 covariace를 줄이는 방법을 사용

<2. K.F. with Probabilistic Approaches>
칼만필터는 확률로 구성.
- 우리의 목표 -> 관측을 토대로 현재 위치를 아는 것.
이는 Markov 특징을 가지고 있다.
- 예측: k-1까지를 이용
- 업데이트: 예측을 이용해 업데이트

<Prediction P(xk|z1k-1)>
Joint Probability를 이용. xk-1 넣기.
Markov System을 이용. P(xk|xk-1,z1k-1)에서 z1k-1제거
- 다이어그램
xk-1이 있기 때문에 zk-1(관측)할 수 있다.
빨간 선은 업데이트.
xk는 xk-1에 영향을 받는다. zk-1은 xk에 영향을 줄 수 없다.
그렇기 때문에 위의 수식에서 z1k-1이 삭제.
*Casual: 인과관계. 어떤 것이 원인이고 결과인지 알려 준다. 원인이 출발 결과가 도착.
이것이 Prediction의 칼만필터의 확률적인 접근.

<Update(Filter) P(xk|z1k)>
P(xk | z1k-1) = P(xk | zk, zk-1): 업데이트를 위해서는 zk만 사용하지 때문에 식을 분리한다.
조건부확률이므로 분수의 형태로 변환.
그리고 여기에 P(xk, z1k-1)을 추가하고 식 정리.
그리고 다시 또 P(z1k-1)을 추가해준다.
첫 번째 정리: P(zk | xk, z1k-1)을 보면 zk에 영향을 주는 것은 오직 xk뿐이다. 즉 z1k-1은 삭제된다. (Conditional Indepence)
두 번째 정리: 분모인 P(zk | z1k-1): 정확하게 풀 길이 없다. 어떤 비율(η)로 변환. k가 변하더라도 일정. Measurement Noise의 확률이 일정하다. 확률적으로 일정한 양이다.
즉, P(xk | z1k-1) = ηP(zk | xk)P(xk | z1k-1)
> 뒤의 P(xk | z1k-1)은 Prediction에서 구한 값
>> 현재(k state)의 z,x의 관계를 이용해서 현재의 state를 업데이트. pred 이용.
어려운 부분은 pred에서 적분 표현이 있다는 점.

<Prediction and Update with Probability>
예측된 결과를 업데이트에 넣고 그 결과를 다시 예측에 넣는다.
예측: 업데이트 * Transitional Probability(확률 형태로 표현되고 모든 형태를 적분)
업데이트는 예측을 만들고 예측이 업데이트를 만든다. (무한 반복)
!!칼만필터의 확률론 기반의 분석!!
- Belief function: 따로 설명X
- 진짜 문제: 적분을 푸는 것이 어렵다. 슬램에서는 다른 형태로 바꾸는 것이 필요.
covariance를 이용한 것이 한 방법.


<Monte Carlo Method>
점의 개수를 세도 1/4확률임을 알 수 있다.
>> 수십개의 입자를 써서 분포를 알게되면 면적을 알 수 있다.
우리가 풀어야할 적분 인자는 확률이다.
입자를 쓰기 때문에 Particle Filter!
입자가 공간상에 어떻게 배치됐는지 보면 면적의 비율을 알 수 있다.
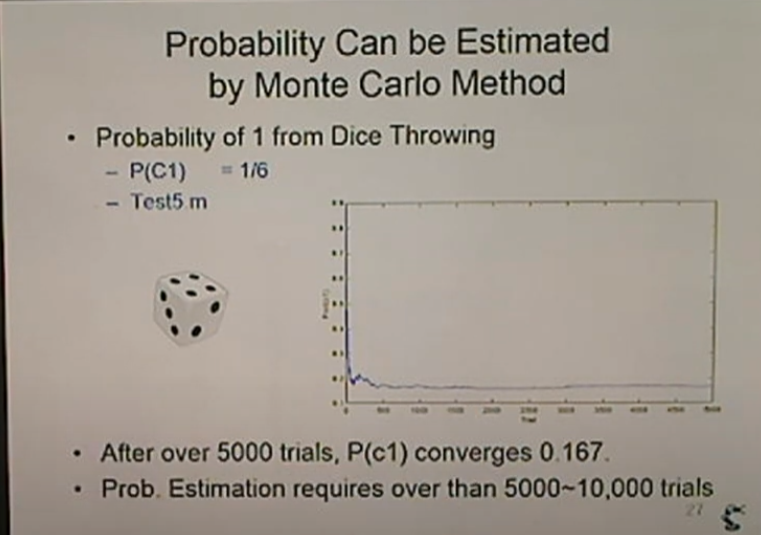
<Probability Can be Estimated by Monte Carlo Method>
주사위를 5000번 던지면 P(c1) = 0.167나온다.
개수를 높일수록 1/6에 근사.

<X with State Model>
<Z with Observation Model>
관측을 통해 보정을 한다.


<We DON'T Know X, but DO Know Z>
Z는 센서를 통해 얻는다.
X를 모르지만 Z는 알 수 있다.
적분을 풀기가 어렵다 -> 다른 방법 시도(입자를 써보자)
xk가 이러한 분포를 가지고 있다. 칼만필터에서는 covariance를 좁히는 것이 목표였다.
xk는 분포를 뜻함. 입자 번호m. 점이 하나 있는데 점이 이동하고 나면 점들의 분포를 가지고 문제를 풀자.
예시: 점이 100개가 있다. 한 스텝 이동하면 점이 펴진다. 이 점의 분포를 가지고 covariacne를 풀면 어떨까? 이것이 기본 컨셉.
fk(점, wk) 를 가지고 covariance를 구하는 기법이 Particle Filter
질문) 점이 이동하면 왜 분포가 퍼질까? Prediction에서는 Process Noise가 없다.
> Process Noise를 추가해야 한다.
Process Noise에 의해서 분포가 커진다.
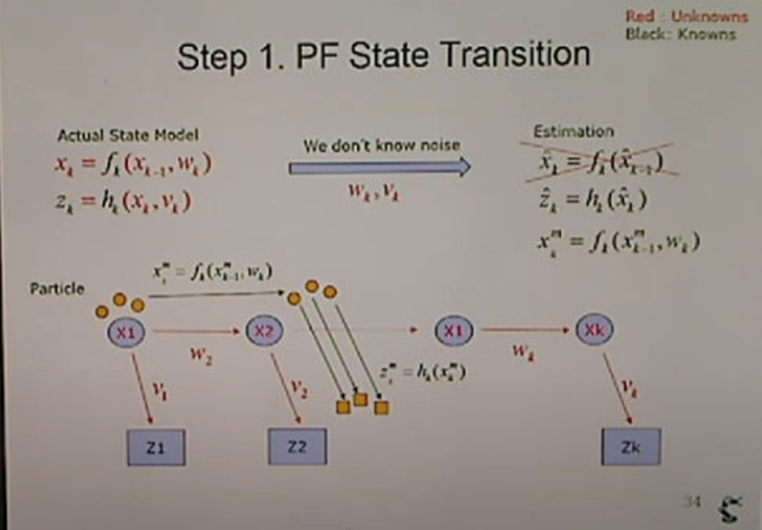

<Step1. PF State Transition>
<Step2. PF Sampling Weight>
점3개가 있다. Process Noise가 있기 때문에 분포가 커진다.
점 3개에 대해 관측을 한다. 네모가 된다.
관측결과를 토대로 covariacne를 구할 수 있다.
관측한 결과를 보고 분포가 되어서 흔들려 있다. 이 중에서 너무 틀린 것은 없앤다.
평균레벨에 가까운 입자만 살린다.

<Step3. PF Resampling>
3개중 멀리 떨어진 2개는 죽인다. 그러면 x좌표는 흐트러진 것들을 모아서 재배치.
입자를 이 근처에 다시 뿌린다. 입자가 3개일때는 covariance가 크지만 모아지게 되면 작아지게 된다.
> 칼만필터에서 covariance를 줄이는 방법과 비슷
주의) 관측한 결과가 실제와 비슷한 값이 있다면 의심해야한다. 너무 좋은 값만 살리면 위험. 좋은 것은 살리지 않는다. 확률분포이기 때문에. 진짜 값이 아닐 가능성이 높다.
Resampling: 좋은 값 주변에 무엇을 살리고 죽일지 재결정하는 것.
뭉쳤다가 다시 조금 벌려준다. (covariance와 같은 경향)
피드백은 언제나 환영합니다.😊
틀린 부분 있다면 지적해주시고 도움이 되었다면 댓글과 공감 눌러주세요
'SLAM' 카테고리의 다른 글
| [SLAM] 양정연 교수 SLAM 강의 34강. Particle Filter (0) | 2022.02.21 |
|---|---|
| [SLAM] 양정연 교수 SLAM 강의 32강. Markov System (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 31강. Joint Probability and Conditional Independence (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 30강. Can we think Kalman Filter with Probability? (0) | 2022.02.21 |
| [SLAM] 양정연 교수 SLAM 강의 29강. From Kalman Filter to Particle Filter (0) | 2022.02.21 |
- Total
- Today
- Yesterday
- AIFFEL인공지능과정
- 모두의연구소
- 아이펠
- AIFFEL후기
- SLAM공부
- 광주인공지능사관학교
- 배달로봇
- AIFFEL
- IT
- 도전
- 해커톤
- 멘탈관리
- 인공지능 교육
- AIFFEL교육
- 모두의 연구소
- 자율주행기술
- 대전 인공지능
- ros
- 인공지능
- Python
- 양정연SLAM
- 멋쟁이사자처럼
- 인공지능교육
- 광주AI
- SLAM강의
- Slam
- 서빙로봇
- 광주
- 실내자율주행
- 자율주행로봇
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
