티스토리 뷰
2021. 10. 26. 23:56
안녕하세요
프로그래밍을 배우는 빛나는 샤트입니다.
SLAM 강의 34강. Particle Filter
*이 포스팅은 목원대학교 양정연 교수님의 SLAM강의 유튜브 영상을 보고 제작되었음을 밝힙니다.
출처: 34강. Particle Filter
34강. Particle Filter
🎉강의요약
1. Particle Filter에서 가장 중요하다고 할 수 있는 Resampling
2. Particle들 중 관측과 비교해 가까운 값들만을 선택하면 다양성이 떨어지기 때문에 이를 보완하기 위해 Resampling 필요
3. 크게 4가지 방법이 있는데 그 중 누적 그래프를 이용한 방법인 Cumulative sum 방식을 이용해 코드 구현
4. 중요한 점1: Measurement(v)가 없다.
5. 중요한 점2: 실제 값을 완벽하게 맞추는 것이 아닌 그 경향을 따라가는 것이 중요하다.
6. 파티클은 최소 200개 이상있어야 성능이 잘 나온다.

<We Don't Know X, but DO Know Z>
파티클 필터 - 칼만 필터와는 방법론적으로 다르다
목표는 같다. 노이즈 적용 부분 다르다.
새로운 X는 함수 F에 영향을 받아서 w와 합쳐서 다음 스텝이 나온다. 현재와 바로 이전 스텝의 값을 이용.
관측자에 의해 z가 나오고 k 스텝의 값을 이용.
Z(관측결과)만을 알고 있을 때 X(위치)를 어떻게 알까? 라는 질문의 답이다.
process/measurement noise를 정확히 모르나 분포는 안다. N(0,1)
X의 분포를 점점 작게 만드는 것이 목표.

<We Don't Know X, but DO Know Z>
^(hat)을 씌워서 추정값을 표현. covariance(분포)로 표현했다. (그림 중 타원 모양)
X라는 점을 정확히 아는 것이 아니라 X 주변의 분포만을 알고 있다.
평균값은 예측된 값.
파티클들을 m개로 구분. X^(추정)을 이용.
covariance를 없애고 하나의 파티클로 본다.
그래서 분포를 여러 개의 파티클들이 모인 것으로 보는 것.
분포를 토대로 covariance를 알아내는 것.

<Step 1. PF State Transition>
각 파티클들은 노이즈(w, 오메가)에 영향을 받아서 진행된다.
파티클 필터에서는 오메가는 가우시간 분포를 가지고 있는데, 하나의 점이 오메가와 f의 영향을 받아서 현재 위치에서 다음 위치로 이동한다.
오메가의 covariance를 randn을 써서 적용.
> 교수님이 싫어하는 부분. 노이즈를 모델링하는 것은 별로. 실제로 흔들려서 퍼지게 된다. 파티클 필터의 장점이자 단점이라고 생각.
단점이라고 생각하는 이유: 오메가가 모델링을 하기에 covariacne가 틀려지게 되면 문제가 커지게 된다. covariance가 다양성을 표현할 수 없다면 문제. 분포가 확실하게 나타나지 않을 수 있다. 파티클은 기본적으로 500~1,000개는 사용해야한다. 그래서 연산량은 꽤 된다.

<Step 2. PF Sampling Weight>
z를 구할 때는 measurement noise를 사용하지 않는다.
> 이유: z주변에 분포가 생긴다. 여기서 따로 v(측정 오차)를 따로 사용하지 않는다. 이미 v(노이즈)가 추가되었다.
관측한 값과 비슷한 파티클들은 w가 크다.


<Step 3. PF Resampling>
관측값과 멀리 떨어지면 버린다.
Resampling: 소수의 좋은 값만 살린다. 1등만 남기는 것은 아니다.
새로운 그룹이 만들어진다.
안 좋은 파티클은 좋은 파티클 위치에 옮겨놓는다.
그림에서 보면 한 군데 파티클이 몰려있으면 위험?
> 다음 스텝에서 특이한 점. 세 개의 파티클이 같은 점에 있다고 해도 오메가가 있기 때문에 퍼진다. 여기서 다시 covariance를 가지게 된다. 관측한 Z값을 이용해 좋은 파티클을 살리는 방식 반복.
파티클들의 평균값을 X^(추정)값이라고 한다.

<Resampling Question??>
w, v를 잘 봐야 한다.
관측 시에 v를 뺀다.
하지만 시그마는 v의 개념을 포함하고 있다.
모든 Xm은 같은 분포를 가지고 있지 않다. 왜?
> 오메가에 의해 분포가 퍼지기 때문.


<Resampling: A Magical Way>
퍼진 양이 오메가의 covariance를 표현.
> 표현을 잘 못한다면 파티클 필터의 성능 낮다.
분포를 결정할 때, 다수와 소수 파티클 그룹이 있다면 다수를 선택하는 것이 아닌 가까운 거리에 있는 그룹을 선택한다.
> 소수라도 에러가 적은 것을 골라야 한다? 문제는 다수가 맞는지 소수가 맞는지 중간중간 확인하기 어렵다.
>> 어떤 것을 버릴지에 대해: 파티클 필터에서의 문제점. 이를 해결하는 하나의 시도가 ROS 내부의 g-mapping.
>>> 이를 해결하기 위한 하나의 방법이 Resampling이다.
예시) 자율주행 차가 잘 가다가 돌멩이에 툭 건드려졌다. 다수가 뒤틀려있을 때 그 다수가 맞을 수도 있다. 즉, 어떻게 Resampling하느냐에 따라 파티클 필터의 성능을 결정한다.

<PF Summary>
Random Particle Generation + Resampling
처음에 랜덤하게 파티클 뿌린다.
오메가의 영향을 받아서 이동.
x^(추정)은 파티클의 평균값.
> 다음 스텝이 나왔다.
이 녀석을 관측z에 넣어준다.
파티클에 대한 z을 얻는다.
주어진 파티클에 대해서 관측한 값의 확률 밀도를 구한다. > w_k
높은 것만 고르는 것이 아닌 Resampling해서 고른다.
이것을 반복.
여기서 w_m은 Importance Sampling Weight.

<PF Example (TestPF.m)>
- System Dynamics 확인. 칼만필터 때 사용했었음.
아래 그래프는 같은 수식인데 다르다.
w가 다르기 때문. (randn으로 생성되기 때문)

<PF Example (TestPF.m)>
관측은 x=z.
관측오차 v를 추가하니 오른쪽과 같이 엄청 튄다.
> 이를 PF로 개선하는 과정

<Simulation for TestPF.m>
- Discretization
미분방정식을 이산화한다.
- w,v를 어떻게 만들까?
randn을 사용.
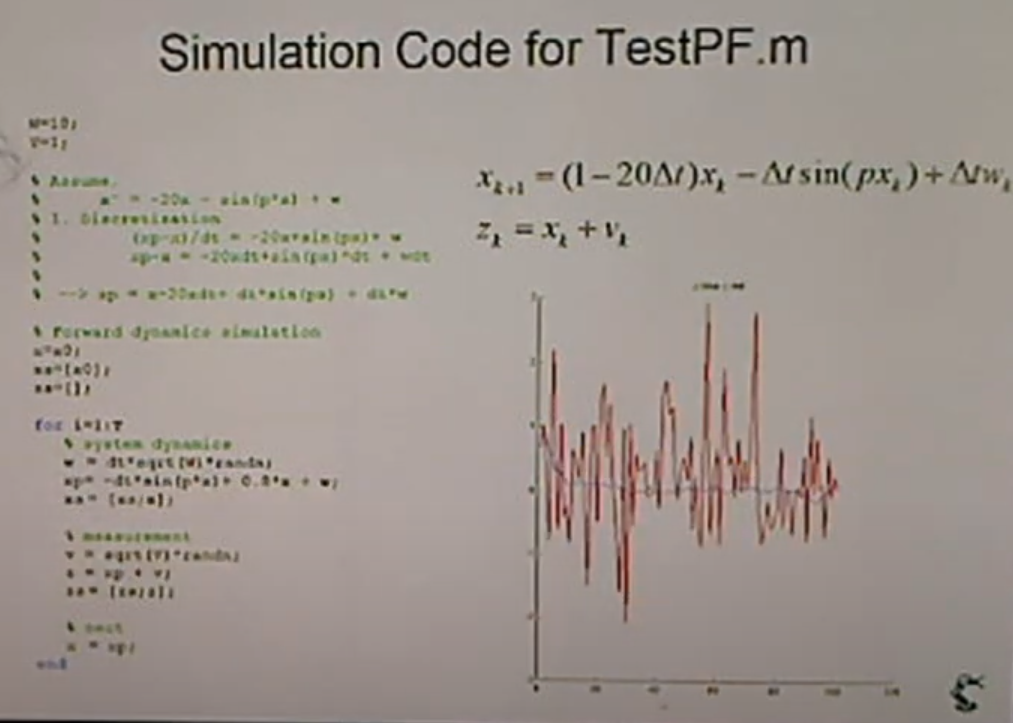
<Simulation Code for TestPF.m>
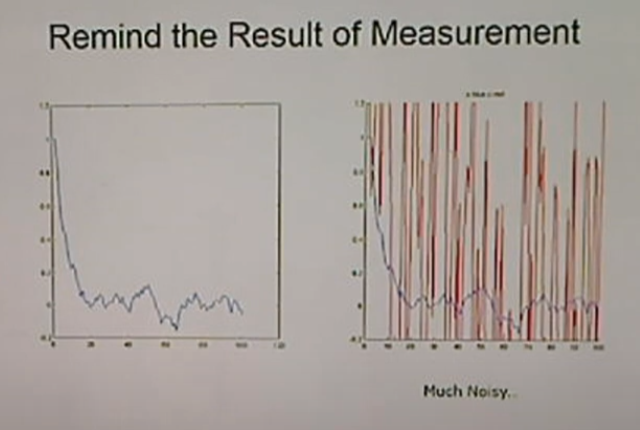
실제로 코드를 구현해보면 관측값(빨간색)이 엄청나게 흔들린다.
하지만 우리가 알고자 하는 것은 파란색.
> 칼만 필터나 파티클 필터를 이용하면 해결 가능

<0. Particle Generation at an Initial State, x0>
초깃값 정의
x = x0
w=10
v=1
for loop은 system dynamics를 표현.
xx는 x값들의 합쳐놓은 array
zx는 빨간색(관측)에 대한 array
> 이제 파티클을 만들어야 한다.
>> 매순간마다 파티클이 퍼져야 한다.
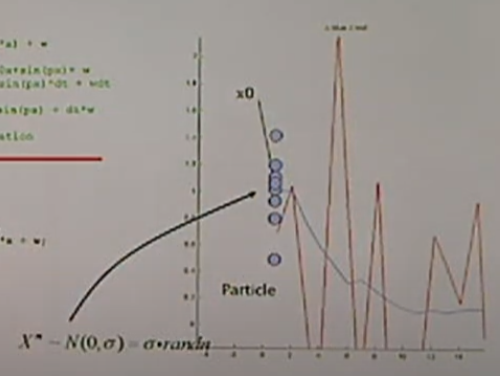
위 그래프를 보면 파티클들이 N(0,1)을 보여준다.
covariance: 퍼져 있는 정도

<testPF2.m>
오메가(w)에 0.01*randn을 적용.
파티클들은 시그마만큼의 분포를 가지고 있다.
중요한 것은 wk(Process Noise)를 가지고 있다.
> 무작위 퍼진 점들이라도 wk때문에 한 스텝만 진행해도 분포의 형태로 변한다.

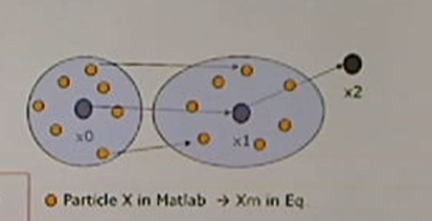
<1. Particle Virtually Moves by System Dynamics>
여기서 파티클은 100개.
process noise는 계속 바뀌어야 한다. (randn 사용)
점들이 이동하게 된다.
관측을 살펴보면 v(Measurement Noise)가 없다.
실제로 시그마를 이용해서 z와 파티클과의 관계를 비교 예정.

<2. Weight Calculation>
z = x + v라고 정의.
P(z|xm) = P(z|zm) 이 성립.
실제 관측한 z가 우측 하단 수식에 들어간다.
Zm들의 분포를 확률밀도함수를 이용해 Z근처의 값들을 살려준다.
모든 weight를 합치면 1이 되도록 수식 구현.
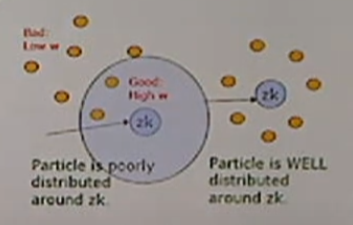
확률 밀도함수를 구해서 보면 가까운 값들만을 이용.

<3. Resampling>
나쁜 값들을 죽이고 좋은 값들 위치로 이동.
Resampling 4가지 방법.
(우측 상단 그림)z(평균값)을 구하고 그 주변에 파티클들이 분포한다면 좋은 결과. Resampling 필요 없다.

<3. Resampling in Matlab>
파티클을 100개.
weight를 확인.
높은 것만 남기면 다양성이 사라진다.
꼭 1등만이 좋은 것은 아니다.
- 다양성 확보를 위한 방법
누적함수를 그린다.
랜덤하게 잘라낸다. 첫번째 높은 값. 두 번째 높은 값을 선택. 이를 반복.
> 대부분의 값들이 살아남게 된다. 다양성 확보.
>> Resampling은 중요하며 크게 4가지가 있는데 위 방법은 Cumulative sum 방식.

<Result: Without Resampling>
점들은 파티클들의 분포.
많이 몰려있는 부분은 거리가 꽤 크다. 에러가 크다.
이유는 파티클이 10개뿐.
process noise가 표현을 잘 못한다.
> 하지만 파티클이 20개라고 하더라도 noise가 엄청 강했다는 것을 잊지말자.

<TestPF2 with N=10>
아래 그래프 확인.
빨간선은 실제
파란선은 예측
파티클 10개여도 나름 잘 따라간다.

<TestPF2 with N=50>
파티클 50개 사용하면, 분포가 평균값과 비슷하게 보인다.
(중요)파란색을 완벽하게 쫓아가는 것이 아니다.
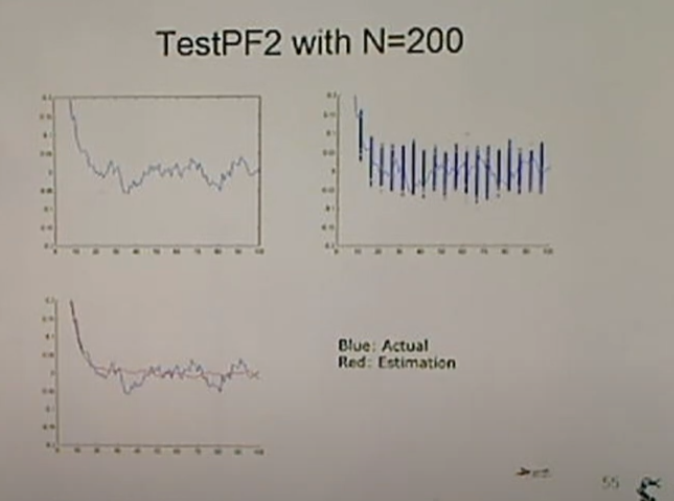
<TestPF2 with N=200>
파티클이 200개.
튀는 노이즈가 있지만 가운데 방향으로 쑤욱 진행하는 것을 확인가능.
200개까지 갔더니 칼만 필터의 결과와 비슷하다.
파티클은 최소 200개 이상이어야 좋은 결과를 얻는다.
피드백은 언제나 환영합니다.😊
틀린 부분 있다면 지적해주시고 도움이 되었다면 댓글과 공감 눌러주세요
'SLAM' 카테고리의 다른 글
- Total
- Today
- Yesterday
- Python
- ros
- 실내자율주행
- 인공지능
- 모두의연구소
- 멘탈관리
- 도전
- AIFFEL인공지능과정
- 서빙로봇
- 멋쟁이사자처럼
- 아이펠
- 양정연SLAM
- 광주AI
- Slam
- AIFFEL교육
- 자율주행로봇
- 광주
- SLAM강의
- 인공지능교육
- 배달로봇
- 광주인공지능사관학교
- AIFFEL후기
- 인공지능 교육
- 해커톤
- 대전 인공지능
- AIFFEL
- 자율주행기술
- SLAM공부
- IT
- 모두의 연구소
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
