티스토리 뷰
- 배치 경사 하강법
- 매개변수 갱신 파이썬 코드
- 모멘텀
- AdaGrad
- Adam
- 가중치 초기값 설정
- Xavier 초기값
- He 초기값
❗매개변수 갱신
❓신경망 학습의 목적은?
> 손실 함수의 값을 최소로 하는 매개변수 값을 찾는 것
>> 최적화(Optimization)
❗최적화하는 방법 중 하나?
> 확률적 경사 하강법(SGD)
>> 매개변수의 기울기를 구해, 기울어진 방향으로 매개변수 값을 갱신하는 작업을 반복해 최적의 값을 찾았음
❗기울기를 구하는 것과 모험가 이야기
> 가장 깊은 골짜기를 찾으려는 모험가는 지도와 시야가 없는 상황에서 지금 서 있는 장소에서 가장 크게 기울어진 방향으로 가는 전략을 세움
>> 이를 반복하다보면 언젠가 '깊은 곳'을 갈 수 있을 것입니다.
>>> 이것이 SGD의 전략
❗SGD(확률적 경사 하강법)
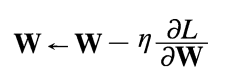
> 왼쪽에 있는 W는 우측의 계산결과로 갱신된다는 의미.
>> (가중치 매개변수) - (학습률 * 가중치 매개변수에 대한 손실 함수의 기울기)
>>> 기울어진 방향으로 일정 거리만 가겠다는 단순한 방법.
❗SGD Python Code
Class SGD:
def __init__(self, lr=0.01): # lr은 학습률
self.lr = lr
def update(self, params, grads): # params, grads는 딕셔너리
for key in params.keys():
params[key] -= self.lr * grad[key]> update 함수를 살펴보면 매개변수[key] == key에 해당하는 값. 즉, 매개변수 딕셔너리 내부의 특정 값(여기서는 W)
> grad[key]는 매개변수 딕셔너리가 가지는 key에 해당하는 값. 즉, 기울기 딕서녀리 내부의 특정 값(W에 대한 손실 함수의 기울기)
> self.lr은 초기화된 학습률
>> 즉, update함수는 매개변수를 갱신해주는 기능

> Optimizer = SGD() 라는 표현은 최적화를 위한 변수 설정
>> 이후 모멘텀이라는 최적화 기법 역시 Momentum()으로 변수를 간단히 설정 가능.
❗SGD 단점


> 방향에 따라 성질이 바뀌는 비등방성 함수에서는 탐색 경로가 비효율적
> 무작정 기울어진 방향으로 진행하는 단순한 방식 (이를 해결하기 위한 방법이 필요해!)
❓왜 지그재그로 움직일까?
> 기울어진 방향이 본래의 최소값과 다른 방향을 가리키고 있기 때문
>> SGD는 기울어진 방향으로 진행하고 모든 데이터를 보려고 하기 때문에 기울어진 방향을 설정하고 최대한 많은 데이터를 보기 위해
------------------------------------------------------------------------------------------------------------------------------------------
⭐SGD(stochastic gradient descent) & BGD(batch gradient descent)
출처 - www.kakaobrain.com/blog/113
- 미니배치 크기에 따른 학습 시간

- 미니배치 크기에 따른 최적화 탐색 경로
1) SGD: 데이터 셋 크기가 N, 미니배치 크기가 1
최적화 함수는 하나의 학습 데이터마다 오차를 계산하며 모델의 가중치를 1 에폭당 N번 갱신
-> 학습이 꼼꼼하게 이뤄짐
-> 시간이 오래 걸림
-> 전체 훈련 데이터의 분포에서 비정상적으로 떨어진 특이값에 따라 가중치 업데이트에 큰 편차가 발생
(특이값에 의해 구해지는 기울기가 실제 최적화 탐색 경로를 크게 벗어나기 때문)
2) BGD: 데이터 셋 크기가 N, 미니배치 크기가 N
최적화 함수는 N개의 데이터를 상대로 오차를 계산하며 모델 가중치를 1 에폭당 1번 갱신
-> 주어진 모든 훈련 데이터의 평균 특성을 파악함으로써 한번의 훈련만으로 최적의 가중치 조합을 제대로 찾아감.

| 미니배치 크기 | 가중치 갱신 per 1epoch | 최적화 탐색 경로 | 비고 | |
| SGD | 1 | N(데이터 셋 크기) | 불안정 | 특이값에 의해 가중치 업데이트 큰 편차 발생 |
| BGD | N(데이터 셋 크기) | 1 | 안정 | 한 번의 훈련만으로 최적의 가중치 업데이트 |
> 결론1: 미니배치가 큰 편이 학습 시간이 빠르고 최적화 탐색 경로 안정적
❓그렇다면 BGD로 다 하면 되는 것 아닐까?
문제1: 미니배치 크기가 크게 되면 모델 최적화(Optimization)와 일반화(generalization) 어렵다.
이유는??
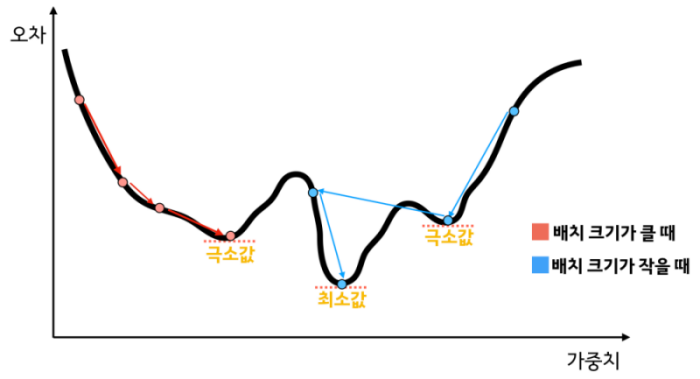
다시 한번 ❓ 최적화란?
> 손실 함수 그래프에서 오차를 최소화하는 가중치 탐색
❗왜 미니배치 크기가 크면 최소값을 찾기 어려울까?
> 비유: 위 그래프를 흘기듯이 스윽 보고 대충 판단하면 '뭐 대충 이정도 기울기면 최소겠네. 결정 땅땅땅' 이렇게 되어 버립니다.
>> 반대의 경우는 데이터 하나하나 살펴보기 때문에 '아 여기가 제일 작은 값이려나...? 좀 더 볼까? 아 역시 더 작은 값이 있었어!' 이렇게 생각하면 될 것입니다. 좀 더 설명을 하면 특이값 데이터로 인해 실제와는 다른 방향의 기울기가 구해지면 가중치 값이 급격하게 변할 가능성이 커지기 때문입니다. (위에서는 특이값때문에 최적화 탐색 경로가 불안정해서 안 좋아보였는데 최적화 측면에선 좋았네요)
❗결론❗
| 미니배치 크기 | 가중치 갱신 per 1epoch | 최적화 탐색 경로 | 비고 | 최적화 | |
| SGD | 1 | N(데이터 셋 크기) | 불안정 | 특이값에 의해 가중치 업데이트 큰 편차 발생 |
극소값에 갇힐 수 있음 |
| BGD | N(데이터 셋 크기) | 1 | 안정 | 한 번의 훈련만으로 최적의 가중치 업데이트 |
최소값을 잘 찾음 |
> 결론2: 학습 시간과 최적화 탐색은 BGD가 우수하나 최적화 측면에서는 좋지 못하다. SGD의 경우 최적화 측면에서는 우수하지만 다른 측면에서는 좋지 못하다.
즉, 미니배치 사이즈를 적절히 설정하는 것(SGD와 BGD 사이)이 매우 중요
------------------------------------------------------------------------------------------------------------------------------------------
⭐모멘텀 - SGD의 단점을 개선해주는 방법 (1)
*모멘텀(Momentum): '운동량'을 뜻하는 단어.

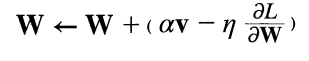
❗모멘텀의 컨셉: SGD 수식에서 av를 더해준 형태
av는 기울기 방향으로 가속을 받아 빠르게 굴러간다는 개념을 도입해 더해주는 값(a는 0.9값 등으로 주로 표현)
v는 물리에서 말하는 속도
class Momentum:
"""모멘텀 SGD"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val) # val와 같은 shape을 가지는 0으로 채워진 array
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]> 파이썬 코드는 SGD와 유사하다.
> updata 함수가 처음 호출될 때 v에 매개변수(params)와 같은 구조의 딕셔너리 변수로 저장
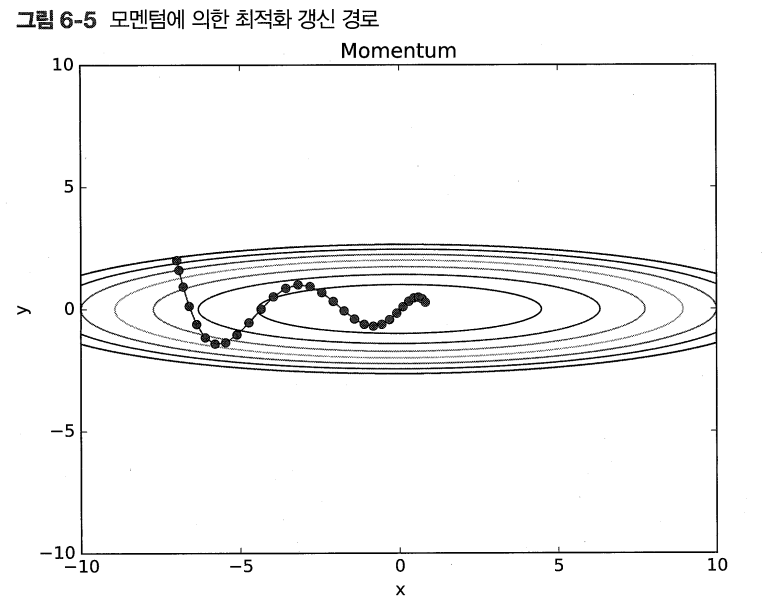
> 모멘텀을 이용하면 SGD보다 x축으로 더 짧은 step을 이용해 이동
> 마치 공이 구르듯 이동
> 하지만 여전히 y축으로는 크게 움직인다.
⭐AdaGrad - SGD의 단점을 개선해주는 방법 (2)
*학습률이 너무 작으면 시간이 오래 걸리고, 너무 크면 발산해 학습이 제대로 이뤄지지 않는다.
*학습률 감소(learning rate decay): 학습 초기에는 크게하다가 조금씩 작게 --> 실제로 쓰임(꽤 좋은 방법)
학습률을서서히 낮추는 방법: 매개변수 '전체'의 학습률 값을 일괄적으로 낮추는 것 --> AdaGrad

새로운 변수 h의 등장: 갱신될때마다 기울기의 제곱이 더해진다.
매개변수 W를 갱신할 때는 1/h^(0.5)를 학습률에 곱해주어 큰 기울기를 가진 매개변수에는 학습률을 작게 만든다
(예시: 갱신된 h가 100일때, W를 갱신할 때 기존 학습률에 1/10이 곱해져 작아지게 된다. 갱신된 h가 더 크다면 학습률은 더 작아짐)
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# 마지막에 1e-7을 더해줘 self.h[key]에 0이 있어도 0으로 나누는 사태 방지*마지막에 1e-7을 더해줘 self.h[key]에 0이 있어도 0으로 나누는 사태 방지

>AdaGrad를 이용하면 SGD에 비해 y축 방향으로 갱신 강도가 약해져 지그재그 움직임 줄어든다.
> x축 방향 step은 SGD와 비슷해보임
*AdaGrad는 과거의 기울기를 제곱해 계속 더해가며 갱신하는데 그러다보면 어느 순간 갱신량이 0이 되어 전혀 갱신이 되지 않는다. 이를 해결하기 위해 먼 과거의 기울기는 잊고 새로운 기울기를 크게 반영하는 RMSProp기법 등장!
⭐Adam - SGD의 단점을 개선해주는 방법 (3)
모멘텀과 AdaGrad를 합치면...? (혹시 끔찍한 혼종이 나오지 않을까?)
그것은 바로 Adam! (since 2015)
*자세한 내용은 기재되어 있지 않고 코드만 확인됨
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
위 코드를 토대로 수식을 작성...했는데 틀릴 수도 있으니 arxiv.org/pdf/1412.6980.pdf 논문에서 확인해보자
(확인은 못했다.)
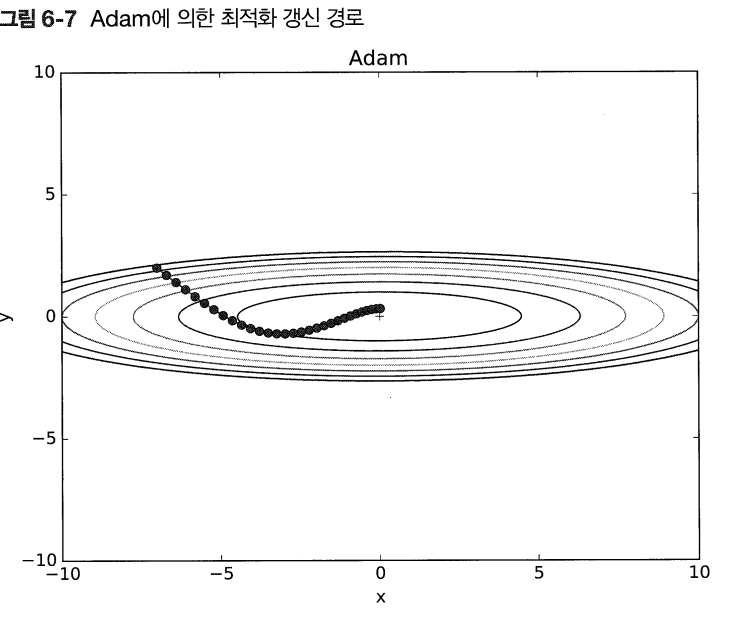
> Adam 이용하게 되면 SGD와는 확연한 차이를 볼 수 있다.
> 모멘텀과 비슷하게 공이 구르듯 움직이지만 좌우 흔들림이 더 적다.
⭐그래서 어떤 방법을 사용할까?

> 여기서는 Adam이 가장 뛰어나 보인다.
> 하지만 풀어야할 문제가 무엇이냐에 따라 달라진다
> 또한 하이퍼파라미터를 어떻게 설정하느냐에 따라 달라진다.
(그때 그때 달라요)
*현재도 SGD를 많이 사용하고 있으며 최근에는 Adam을 많이 사용하는 추세로 보임(저자 의견)
⭐손글씨 데이터(MNIST)로 본 갱신 방법 비교
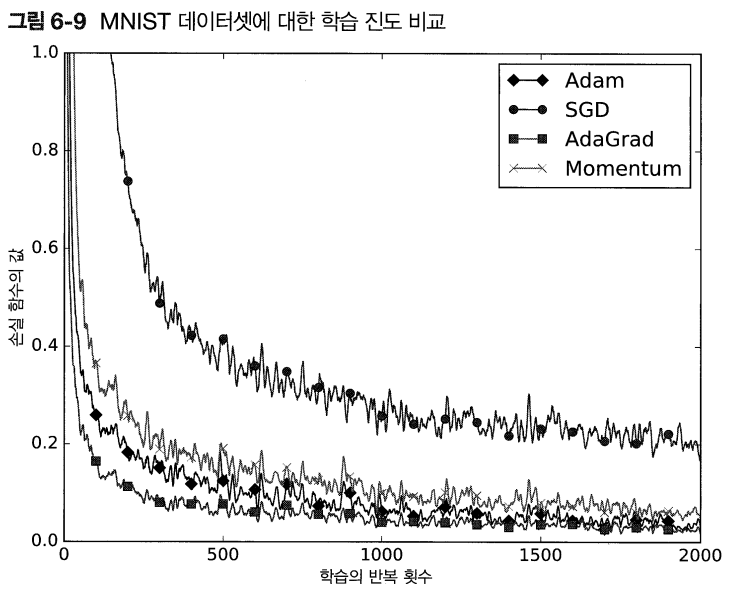
> SGD: 학습 진도가 가장 느리다
> 나머지 세 개는 비슷해 보임. AdaGrad가 가장 빠른 것으로 판단
>> 하이퍼파라미터(학습률, 신경망의 구조)에 따라 달라질 수 있다.
>>> 일반적으로 SGD보다 다른 세 기법이 빠르게 학습하고, 때로는 최종 정확도도 높게 나타남.
❗가중치의 초기값
❓ 가중치의 초기값이 중요한 이유는?
> 신경망 학습의 성패가 갈린다.
⭐가중치 감소와 오버피팅
> 오버피팅을 억제해 성능을 올리는 '가중치 감소'
> 가중치 감소: 가중치 매개변수의 값이 작아지도록 학습하는 방법
❓그러면 최대한 작은 값(0)으로 시작하면 되지 않을까?
정확히는 가중치를 균일한 값으로 설정하는 행위
> 왜 안될까요?
>> 예를 들어 2층 신경망에서 둘 다 가중치가 0이라면 가중치가 갱신되지 않는다.
>> 가중치를 여러개 가지는 의미를 상실
>>> 초기값은 무작위로 설정
❗가중치 초기값과 은닉층의 활성화값
> 층 5개, 각 층의 뉴런 100개, 입력 데이터 1,000개를 정규분포로 무작위로 생성
> 활성화 함수는 시그모이드
> 활성화 결과를 히스토그램으로 표현 (표준편차에 따라 변화를 보고자 함, 현재는 표준편차 = 1)

>> 표준편차 1일 때: 0과 1에 치우침
>>> 역전파의 기울기 값이 점점 작아지다가 사라짐: 기울기 소실 --> 딥러닝에서 큰 문제!
> 표준편차 = 0.01일때 결과

>> 표준편차 0.01일 때: 0.5부근에 집중
>> 기울기 소실 문제는 없으나 치우졌다는 뜻은 다수의 뉴런이 같은 값을 가지고 있다 --> 뉴런을 여러 개 둔 의미가 없다.
>>> 표현력이 제한되는 문제 발생
⭐Xavier 초기값
> 이 초기값의 목적: 각 층의 활성화값들을 광범위하게 분포 --> 가중치의 적절한 분포 찾기 위해
> 방법: n개의 노드가 있다면 표준편차가 1/n^0.5인 분포 사용

>> 위 수식에서 알 수 있듯이 앞 층에 노드가 많을수록 대상 노드의 초기값으로 설정하는 가중치가 좁게 퍼짐

> 층이 깊어질수록 (형태가 다소 일그러지지만) 확실히 앞에서 본 방법보다 더 넓게 분포!
❗ReLU사용할 때의 가중치 초기값
> 카이밍 히가 찾아낸 He초기값
>> 앞 계층의 노드가 n개일 때, 표준편차가 (2/n)^0.5사용

> 표준편차 = 0.01인 정규분포, Xavier 초기값, He초기값 사용한 경우
>> 표준편차 = 0.01인 정규분포: 각 층의 활성화 값이 매우 작다 --> 역전파 때 가중치 기울기가 작다 --> 학습이 거의 되지 않는다.
>> Xavier 초기값: 층이 깊어지면서 치우침이 커짐 --> 기울시 소실 문제 발생
>> He 초기값: 모든 층에서 균일하게 분포 --> 역전파 때도 적절한 값이 나옴
🔥초기값에 대한 결론: ReLU를 사용할 때는 He 초기값 사용, 시그모이드 또는 tanh 등의 S자 모양 곡선일 때는 Xavier 초기값 사용
'ML DL' 카테고리의 다른 글
| [지시딥] chapter6. 배치 정규화, 드롭아웃, 하이퍼파라미터 갱신 p210~226 (0) | 2022.02.16 |
|---|---|
| [지시딥] SGD와 BGD 그리고 학습 (0) | 2022.02.16 |
| [논문읽기][STARK]Learning Spatio-Temporal Transformer for Visual Tracking (0) | 2022.02.16 |
| [논문읽기][SSD]Single Shot MultiBox Detector (0) | 2022.02.16 |
| [논문읽기][EfficientNet]Rethinking Model Scaling for Convolutional Neural Networks (0) | 2022.02.16 |
- Total
- Today
- Yesterday
- SLAM강의
- 배달로봇
- AIFFEL
- AIFFEL교육
- 멋쟁이사자처럼
- IT
- 아이펠
- 인공지능
- ros
- 광주인공지능사관학교
- 광주AI
- 인공지능교육
- 자율주행기술
- 대전 인공지능
- 도전
- 실내자율주행
- 멘탈관리
- SLAM공부
- 해커톤
- AIFFEL후기
- 양정연SLAM
- 광주
- 모두의 연구소
- 자율주행로봇
- Slam
- 인공지능 교육
- 서빙로봇
- AIFFEL인공지능과정
- 모두의연구소
- Python
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
