티스토리 뷰
활성화값 분포가 적당히 퍼지면서 원활한 학습
- 각 층이 활성화를 적당히 퍼뜨리도록 '강제'
6.3.1 배치 정규화 알고리즘
- 학습을 빨리 진행할 수 있다
- 초기값에 크게 의존하지 않는다
- 오버피팅을 억제한다

*배치 정규화: 학습 시 미니배치 단위로 정규화. 데이터 분포가 평균이 0, 분산이 1.

위 식은 단순히 미니배치 입력 데이터 {x1, x2, ..., xm}을 평균0, 분산1인 데이터로 변환.
이를 활성화 함수 앞(또는 뒤)에 삽입 --> 데이터 분포가 덜 치우치게 만들 수 있다.
*배치 정규화 계층마다 이 정규화된 데이터에 고유한 확대와 이동변환을 수행


*신경망의 순전파에서 적용되는 계산 그래프(그림 6-17)
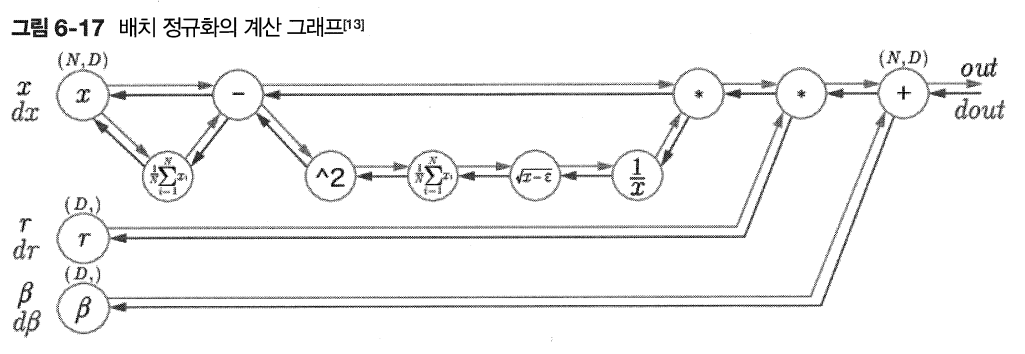
6.3.2 배치 정규화의 효과
- MNIST 데이터셋을 이용해 배치 정규화 계층 사용 유무에 따른 학습 진도 변화 확인

>> 배치 정규화가 학습을 빨리 진전시키고 있다.
*초기값 분포를 다양하게 --> 학습 진행 확인
(예시: 가중치 초기값의 표준편차를 다양하게 바꾸면서 학습 경과의 그래프)

>> 거의 모든 경우에서 배치 정규화를 사용할 때 학습 진도가 빠르다!
>> 실제로 배치 정규화를 이용하지 않는 경우엔 초기값이 잘 분포되지 않으면 학습 진행❌
❗배치 정규화 사용 --> 학습이 빨라지며, 가중치 초기값에 크게 의존❌
6.4 바른 학습을 위해
*범용 성능: 아직 보지 못한 데이터가 주어져도 바르게 식별해내는 능력
*오버피팅: 신경망이 훈련 데이터만 지나치게 적응되어 그 외의 데이터에는 제대로 대응하지 못함
6.4.1 오버피팅
- 아래의 경우에 주로 발생
1) 매개변수가 많고 표현력이 높은 모델
2) 훈련 데이터가 적음
( 아래 예시는 두 조건을 모두 적용시켜 일부러 오버피팅을 일으킴 )
( 60,000개 데이터셋 중 훈련 데이터 300개만 사용, 7층 네트워크 사용, 각 층 뉴런 100개, 활성화 함수:ReLU)
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 오버피팅을 재현하기 위해 학습 데이터 수를 줄임
x_train = x_train[:300]
t_train = t_train[:300]
# weight decay(가중치 감쇠) 설정 =======================
#weight_decay_lambda = 0 # weight decay를 사용하지 않을 경우
weight_decay_lambda = 0.1
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01) # 학습률이 0.01인 SGD로 매개변수 갱신
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
# 그래프 그리기==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

>> 훈련 데이터를 사용하여 측정한 정확도는 100 에폭을 지나면서 거의 100%.
>> 하지만 시험 데이터와는 큰 차이를 보인다.
>>> 이는 훈련데이터만 적응해서 시험 데이터에서는 낮은 정확도가 나오는 오버피팅 발생!
6.4.2 가중치 감소
*오버피팅 억제를 위한 방법 중 하나
- 학습 과정에서 큰 가중치에 대해서 그에 상응하는 큰 패널티를 부과
( 오버피팅의 원인: 가중치 매개변수의 값이 커서 발생하는 경우가 많다 )



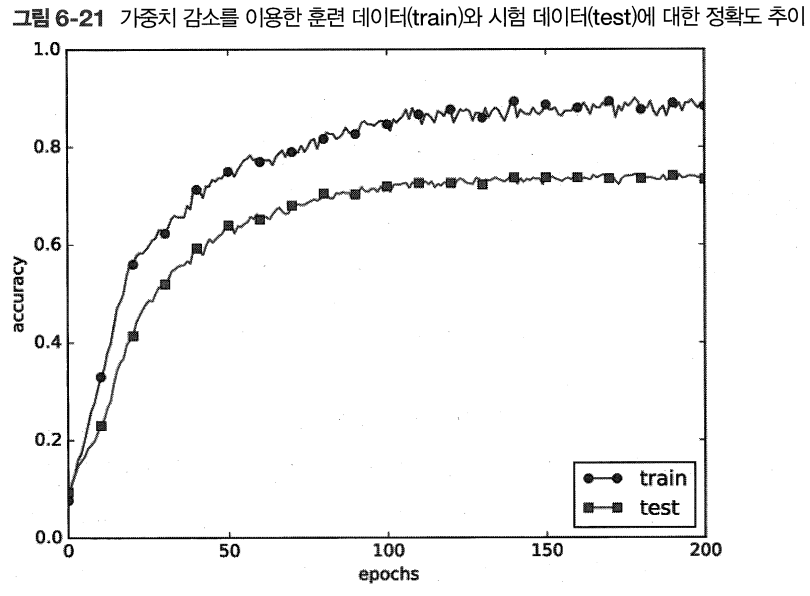
>> 여전히 훈련 데이터에 대한 정확도와 시험 데이터에 대한 정확도가 차이가 있지만 이전보다 오버피팅 억제!
또한 훈련 데이터에 대한 정확도가 100%에 도달하지 못함
6.4.3 드롭아웃
앞서 배운 내용(손실 함수에 가중치의 L2 법칙을 더한 가중치 감소 방법)은 간단하게 구현가능하지만
어느 정도 지나친 학습을 억제할 수 있다.
그러나 신경망 모델이 복잡해지면 가중치 감소만으로 대응하기 어렵다 -- > 드롭아웃 사용!
*뉴런을 임의로 삭제하면서 학습하는 방법
- 훈련 때 은닉층의 뉴런을 무작위로 골라 삭제(삭제된 뉴런은 신호를 전달하지 않는다)
- 시험 때는 모든 뉴런에 신호를 전달(각 뉴런의 출력에 훈련 때 삭제한 비율을 곱해 출력)

Class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask>> 순전파를 담당하는 forward메서드에서는 훈련 때(train_flg = True일 때)만 잘 계산해두면 시험 때는 단순히 데이터를 흘리기만 하면 된다. 삭제한 비율은 곱하지 않아도 좋다(실제로도 안 한다)
>> 핵심은 순전파 때마다 self.mask에 삭제할 뉴런을 False로 표시하는 것!
>> self.mask는 x와 형상이 같은 배열을 무작위롤 생성하고 그 값이 dropout_ratio보다 큰 원소만 True로 설정
>> 역전파 때의 동작은 ReLU와 같다.
>>> 순전파 때 신호를 통과시키는 뉴런은 역전파 때도 신호를 그대로 통과, 통과시키지 않는 뉴런은 역전파 때도 신호를 차단
- 드롭아웃 효과 확인(MNIST 데이터셋)

>> 드롭아웃을 적용 결과(우측 그래프): 훈련 데이터와 시험 데이터에 대한 정확도 차이가 줄었다.
>> 또한 훈련데이터에 대한 정확도가 100%에 도달하지 않음!
>>> 드롭아웃을 이용하면 표현력을 높이면서 오버피팅 억제 가능

6.5 적절한 하이퍼파라미터 값 찾기
하이퍼파라미터: 각 층의 뉴런 수, 배치 크기, 매개변수 갱신 시의 학습률과 가중치 감소 등 사용자가 직접 설정해줘야 하는 값
> 적절한 하이퍼파라미터 값을 잘 설정하는 것이 매우 중요
6.5.1 검증 데이터
!주의!
하이퍼파리미터의 성능을 평가할 대는 시험 데이터를 사용해서 안 된다!
> 이유: 시험 데이터를 이용하게 되면 시험 데이터에 오버피팅이되기 때문
* 검증 데이터: 하이퍼파라미터의 적절성을 평가하기 위한 데이터셋
*훈련 데이터: 매개변수 학습
*검증 데이터: 하이퍼파라미터 성능 평가
*시험 데이터: 신경망의 범용 성능 평가
(x_train, t_train), (x_test, t_test) = load_minst()
# 훈련 데이터를 섞는다.
x_train, t_train = shuffle_dataset(x_train, t_train)
# 20%를 검증 데이터로 분할
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]> 이 코드는 훈련 데이터를 분리하기 전에 입력 데이터와 정답 레이블을 섞는다.
(혹시 데이터셋이 한쪽으로 치우쳐있는 경우가 있을 수 있기 때문)
6.5.2 하이퍼파라미터 최적화
> 하이퍼파라미터의 '최적값'이 존재하는 범위를 조금씩 줄여가는 것
>> 대략적인 범위 설정 - 무작위로 하이퍼파라미터 선정(샘플링) - 그 값으로 정확도 평가
위 작업을 반복
<하이퍼파라미터 최적화 단계>
0단계: 하이퍼파라미터 값의 범위 설정
1단계: 설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출
2단계: 1단계에서 샘플링한 하이퍼파라미터 값을 사용하고 학습하고, 검증 데이터로 정확도 평가
3단계: 1단계와 2단계를 특정 횟수(100회 등) 반복하며, 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힌다.

6.5.3 하이퍼파라미터 최적화 구현하기
- 하이퍼파라미터의 검증은 그 값을 0.001~1,000 사이 같은 로그 스케일 범위에서 무작위 추출
10 ** np.random.uniform(-3,3) # 0.001 ~ 1,000 범위
- 가중치 감소 계수를 10^-8 ~ 10^-4, 학습률을 10^-6 ~ 10^-2 범위에서 시작
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 1- ** np.random.uniform(-6, -2)
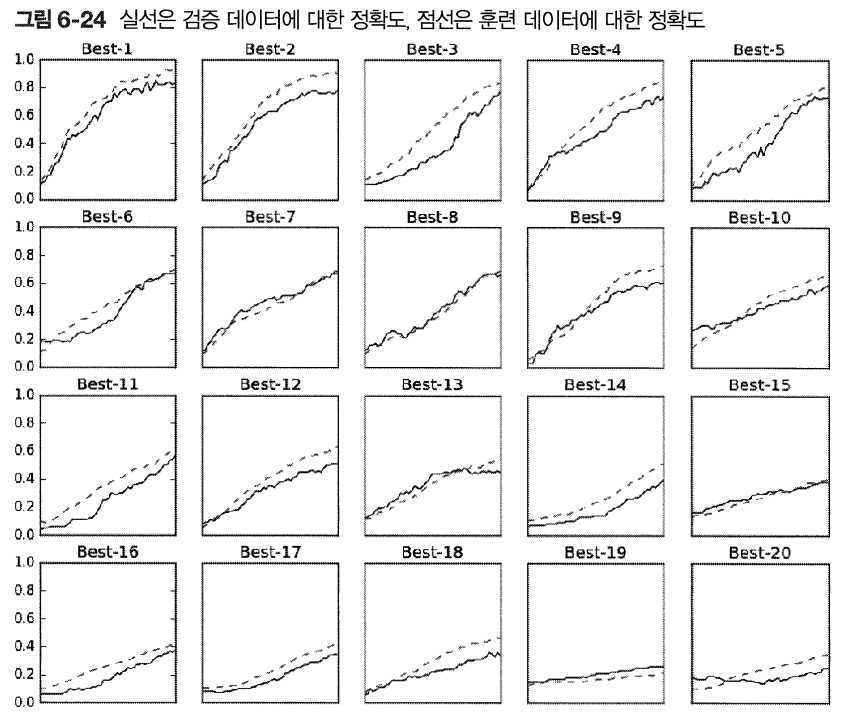
> 위의 결과를 보면 Best-5까지는 학습이 잘 되고 있는 추세
>> Best-5까지 하이퍼파라미터의 값(학습률과 가중치 감소 계수) 살펴보기

>>> 학습률은 0.001 ~ 0.01, 가중치 감소 계수는 10^-8 ~ 10^-6
>>> 이처럼 잘될 것 같은 값의 범위를 관찰하고 범위를 좁힌다. 이를 반복
6.6 정리
*매개변수 갱신 방법에는 확률적 경사 하강법(SGD)외에도 모멘텀, AdaGradm, Adam 등이 있다.
*가중치 초기값을 정하는 방법은 올바른 학습을 하는 데 매우 중요
*가중치의 초기값으로는 'Xavier 초기값'과 'He 초기값'이 효과적
*배치 정규화를 이용하면 학습을 빠르게 진행 + 초기값에 영향을 덜 받는다
*오버피팅을 억제하는 정규화 기술 --> 가중치 감소 & 드롭아웃
*하이퍼파라미터 값 탐색은 최적 값이 존배할 법한 범위를 점차 좁히면서 하는 것이 효과적
'ML DL' 카테고리의 다른 글
| [지시딥2] RNN을 사용한 문장 생성 p289 ~ 310 (0) | 2022.02.16 |
|---|---|
| [지시딥] SGD와 BGD 그리고 학습 (0) | 2022.02.16 |
| [지시딥] chapter 6 .학습 관련 기술들(p189~208) (0) | 2022.02.16 |
| [논문읽기][STARK]Learning Spatio-Temporal Transformer for Visual Tracking (0) | 2022.02.16 |
| [논문읽기][SSD]Single Shot MultiBox Detector (0) | 2022.02.16 |
- Total
- Today
- Yesterday
- AIFFEL
- 자율주행기술
- 광주
- SLAM공부
- 아이펠
- 양정연SLAM
- 실내자율주행
- 자율주행로봇
- SLAM강의
- 대전 인공지능
- 모두의 연구소
- 서빙로봇
- 도전
- 인공지능
- 해커톤
- 광주AI
- 멘탈관리
- 인공지능교육
- Python
- Slam
- AIFFEL교육
- AIFFEL후기
- 인공지능 교육
- IT
- 멋쟁이사자처럼
- AIFFEL인공지능과정
- 모두의연구소
- ros
- 광주인공지능사관학교
- 배달로봇
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
